Что такое группа виды групп: определение и основные характеристики

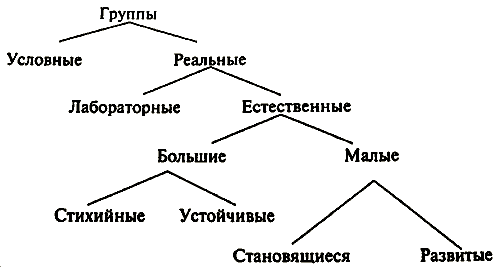
Группа виды групп – это понятие, широко используемое в различных областях науки, включая биологию, социологию, психологию и др. Это концепция, которая помогает понять и изучить взаимодействие и организацию различных сущностей, объединенных общими характеристиками или целями.

Основная идея группы виды групп заключается в том, что сущности, находящиеся внутри группы, обладают определенными свойствами или особенностями, которые отличают их от сущностей, находящихся за ее пределами. Группы виды групп могут быть формальными или неформальными, созданными специально для достижения определенных целей или возникающими естественным образом в результате взаимодействия людей или организаций.

Один из основных аспектов групп виды групп – это их структура. Группы виды групп могут иметь иерархическую структуру, где каждая сущность занимает определенное место и выполняет определенные функции. Кроме того, группы виды групп могут быть открытыми или закрытыми, что означает, что они могут принимать новых участников или быть ограниченными в количестве участников.

Важно отметить, что группы виды групп могут иметь сильное влияние на поведение и развитие индивидуумов. Они могут быть местом, где люди находят поддержку, мотивацию и идеи, а также местом, где происходит конкуренция, соперничество и конфликты.

Группы виды групп – это сложное явление, требующее детального изучения и анализа. Они играют важную роль в обществе и культуре, в процессе принятия решений, достижении целей и формировании личности. Понимание основных характеристик и свойств групп виды групп позволяет нам лучше понять и объяснить многие аспекты нашего мира и взаимодействия с ним.

Определение группы виды групп

Группа виды групп — это определенное множество видов, объединенных общими характеристиками и особенностями. Это понятие используется в биологии для классификации организмов и позволяет систематизировать их разнообразие.

Одним из основных критериев группировки видов является их сходство по строению и функциональности. Виды, объединенные в группу, обладают схожими анатомическими и физиологическими особенностями, что свидетельствует о их близком родстве и общем эволюционном происхождении.

Также группы виды групп могут основываться на общих экологических адаптациях. Например, виды, живущие в одном и том же биотопе или обладающие схожими пищевыми предпочтениями, могут объединяться в группу для изучения их взаимодействия в данной экологической нише.

Важным критерием группировки видов является таксономическое родство. Виды, находящиеся на одном уровне в таксономической иерархии (например, одна семья или один род), могут составлять группу для сравнительного анализа и изучения их общих и отличительных признаков.

Использование групп виды групп помогает упорядочить и классифицировать биологическое разнообразие. Это позволяет более глубоко изучать отдельные виды, а также понимать их взаимосвязи и эволюционные тенденции. Кроме того, классификация в группы позволяет упростить систематические работы и более эффективно управлять биологическими ресурсами.

Роль группы виды групп в теории симметрии

Группа виды групп – это основной инструмент в теории симметрии, который позволяет изучать и классифицировать различные виды симметрий в физике и математике. Группа виды групп состоит из набора симметричных преобразований, которые сохраняют заданный объект или систему. Она играет ключевую роль в построении моделей и теорий, объясняющих различные явления и законы природы.

Группы виды групп классифицируются по своим основным характеристикам, таким как число элементов, законы композиции и свойства симметрии. Они могут иметь различные размерности и структуру, что предоставляет возможность рассмотрения различных аспектов симметрии в различных физических системах. Эти группы позволяют описывать, анализировать и предсказывать симметрию объектов и явлений, а также предоставляют математическую основу для решения сложных проблем и задач.

Ключевая особенность группы виды групп заключается в ее универсальности и применимости. Она может быть применена в различных областях науки, включая физику элементарных частиц, квантовую механику, кристаллографию, химию и даже биологию. Группа виды групп позволяет исследовать симметрию и закономерности, которые сохраняются в различных системах, и создавать более точные модели, которые объясняют наблюдаемые явления и свойства материи.

Структура группы виды групп

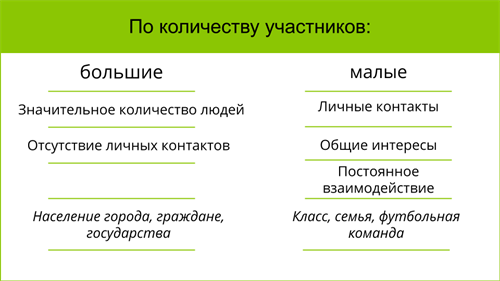
Группа виды групп представляет собой форму организации и социального взаимодействия, где осуществляется совместное деятельность индивидуумов с целью достижения определенных результатов. Структура группы виды групп описывает основные элементы и связи, которые присутствуют в ее организации.

Основными характеристиками структуры группы виды групп являются: роли, нормы и статусы. Роль представляет собой социальную позицию, которую индивиды занимают внутри группы. Каждая роль имеет свои задачи, обязанности и ожидания. Нормы представляют собой правила и ожидания, которыми группа регулирует поведение своих участников. Статус определяет социальное положение индивида в группе и влияет на его влияние и привлекательность.

Структура группы виды групп может быть представлена в виде иерархии, где есть лидеры и подчиненные. Лидеры обладают большим влиянием и властью, их решения и действия влияют на остальных участников группы. Подчиненные следуют указаниям и инструкциям лидеров. Эта иерархическая структура позволяет более эффективно организовывать деятельность и достигать поставленных целей.

Структура группы виды групп также может быть представлена в виде сети, где участники группы взаимодействуют напрямую друг с другом, не зависимо от их роли или статуса. Эта структура способствует свободному обмену информацией и идеями, что может повысить креативность и результативность группы.

Различные виды групп могут иметь разные структуры в зависимости от целей, задач и контекста. Важно учитывать особенности группы и подбирать наиболее эффективную структуру для достижения поставленных целей.

Основные характеристики группы виды групп

Группа виды групп — это организованное объединение людей, основанное на общественных отношениях и обладающее определенными характеристиками. Одной из основных характеристик группы виды групп является ее размер. Группы виды групп могут быть маленькими, с несколькими участниками, или большими, включающими сотни или даже тысячи людей.

Важной характеристикой группы виды групп является ее цель. Группа виды групп может объединяться для достижения общей цели, такой как реализация проекта или решение общей проблемы. Также группа виды групп может иметь свои собственные цели, связанные с особыми интересами или потребностями ее участников.

Другой важной характеристикой группы виды групп является степень социальной связанности. Группы виды групп могут быть более или менее связанными между собой. Высокая степень связанности подразумевает сильные социальные связи и взаимодействие между участниками, что способствует эффективности работы группы. Низкая степень связанности может означать, что участники группы виды групп мало общаются друг с другом или имеют различные взгляды и интересы.

Также группа виды групп может быть формальной или неформальной. Формальная группа виды групп имеет четко определенные структуры и роли, а участники такой группы обязаны соблюдать определенные правила и нормы. Неформальная группа виды групп, напротив, не имеет строгих правил и структур, участники взаимодействуют на основе своих отношений и собственных предпочтений.

Понятие субгруппы группы виды групп

Субгруппа – это подмножество элементов группы, которое само является группой относительно той же операции, заданной на исходной группе. То есть, если обозначить группу как (G, *), то субгруппой будет множество элементов H, которое является группой относительно операции *, наследуемой от главной группы G.

Субгруппа обладает рядом основных характеристик, которые определяют ее свойства. Во-первых, в состав субгруппы должны входить нейтральный элемент и обратные элементы для всех элементов субгруппы. Также, субгруппа должна быть замкнута относительно операции группы, то есть результат операции двух элементов из субгруппы также должен принадлежать субгруппе.

Одной из основных характеристик субгруппы является ее порядок, который определяется количеством элементов в субгруппе. Порядок субгруппы всегда является делителем порядка группы. Также, если субгруппа является конечнопорожденной, то она может быть представлена как линейная комбинация основных элементов, называемых образующими, с коэффициентами из множества целых чисел.

Одна из основных задач изучения субгрупп — это определение их связи с фактор-группами. Если рассмотреть фактор-группу как множество левых смежных классов по отношению к субгруппе, то получится новая абстрактная группа с операцией, определенной на основе операции изначальной группы.

Примеры групп виды групп

1. Профессиональные группы: В данную категорию входят группы, объединяющие людей с общим профессиональным интересом или деятельностью. Например, группы программистов, экономистов, врачей и т.д. Эти группы предоставляют своим участникам возможность обмениваться опытом, задавать вопросы, обсуждать новые технологии и находить единомышленников.

2. Интересные группы: Это группы, созданные для людей с общим интересом к определенным темам или хобби. Например, группы любителей фотографии, путешествий, спорта и т.д. В таких группах участники могут делиться своими фотографиями, обсуждать новые места для путешествий, обмениваться опытом и находить единомышленников.

3. Образовательные группы: В эти группы входят студенты и преподаватели, объединенные общим образовательным процессом. Группы могут создаваться для конкретных учебных курсов, школ или университетов. В таких группах участники могут обмениваться учебными материалами, задавать вопросы, обсуждать темы занятий и т.д.

4. Работнические группы: Это группы, созданные для обсуждения профессиональных вопросов и проблем на рабочем месте. Например, группы сотрудников одного отдела или предприятия. В таких группах участники могут обсудить текущие задачи, обменяться мнениями, решить проблемы и повысить эффективность работы.

5. Социальные группы: В данную категорию входят группы, основанные на общих социальных интересах или целях. Например, группы, объединяющие людей, занимающихся благотворительностью, защитой прав животных, защитой окружающей среды и т.д. В таких группах участники могут обмениваться информацией, организовывать совместные мероприятия и вместе работать над реализацией своих социальных целей.

Важность групп виды групп в математике

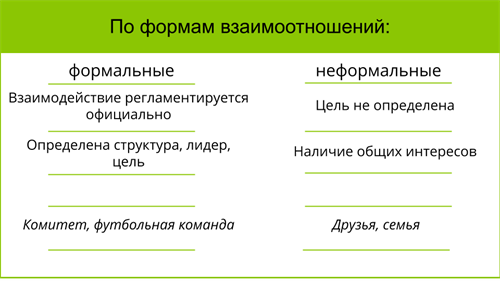
Группы виды групп являются одним из основных объектов изучения в алгебре и теории групп. В математике группы виды групп используются для анализа и классификации групп. Изучение их свойств позволяет лучше понять структуру групп и разработать методы для их анализа.

Группы виды групп широко применяются не только в математике, но и в других областях науки, таких как физика, химия и информатика. Например, в физике группы виды групп используются для описания симметрий физических систем, а в химии — для классификации молекул по их симметрии и свойствам.

Изучение групп виды групп играет важную роль и в прикладной математике. Например, в криптографии группы виды групп применяются для разработки алгоритмов шифрования и защиты информации. Также группы виды групп используются в компьютерной графике для создания и анимации трехмерных объектов.

В итоге, группы виды групп являются неотъемлемой частью математики и имеют широкий спектр применений в различных областях науки и техники. Изучение их свойств и характеристик позволяет строить новые математические модели, разрабатывать новые методы и алгоритмы, а также решать практические задачи в различных областях жизни.

Применение групп виды групп в физике

В физике группы виды групп широко применяются для описания симметрий в физических системах. Одна из основных областей, где применяются группы виды групп, — это квантовая физика. В квантовой физике группы виды групп используются для описания симметрий элементарных частиц, таких как кварки и лептоны.

Группы виды групп также применяются для анализа и классификации кристаллических структур. Кристаллические структуры могут иметь различные симметрии, которые могут быть описаны с помощью определенных групп виды групп. Это позволяет упростить и систематизировать изучение свойств кристаллов и их влияние на физические процессы.

Также группы виды групп используются в физике элементарных частиц для описания симметрий фундаментальных взаимодействий, таких как сильное и электромагнитное взаимодействия. Эти симметрии могут быть описаны с помощью специальных групп виды групп, таких как группы Ли или группы калибровочной симметрии.

Кроме того, группы виды групп применяются при изучении физики столкновений частиц. Они помогают анализировать симметрии и законы сохранения, которые проявляются во время столкновений частиц. Это позволяет предсказывать результаты столкновений и изучать физические законы, которые работают на микроуровне.

Группы виды групп в криптографии

В криптографии группы являются важным инструментом для обеспечения безопасности информации. Существуют различные виды групп, которые используются в криптографических протоколах и алгоритмах.

Одним из наиболее распространенных типов групп в криптографии являются абелевы группы. В абелевой группе операция комбинирования элементов коммутативна, то есть порядок сложения элементов не имеет значения. Это делает абелевы группы особенно полезными в криптографии, так как позволяет легко выполнять операции секретного ключа, такие как сложение и умножение.

Еще одним типом групп, широко использующимся в криптографии, являются группы перестановок. Группы перестановок являются симметричными группами, в которых элементы представляют собой перестановки элементов множества. Они позволяют выполнять перестановки битовых последовательностей, что является одной из основных операций в современных шифрах.

Кроме того, в криптографии встречаются и другие виды групп, такие как группы Эйзенштейна и линейные группы. Группы Эйзенштейна используются, например, в алгоритмах криптографического подписывания, а линейные группы — в алгоритмах шифрования и декодирования.

В заключение, группы играют важную роль в криптографии, обеспечивая безопасность передаваемой информации. Различные виды групп позволяют выполнять различные операции и алгоритмы, что делает их неотъемлемой частью шифрования и защиты данных.