Как использовать квадрат Декарта для принятия решений: практическое руководство

В современном быстротечном мире принятие решений играет важную роль в нашей повседневной жизни. От выбора карьеры до решения, где провести выходные, каждый день мы сталкиваемся с множеством выборов. Квадрат Декарта, также известный как матрица принятия решений, предоставляет удобный и систематический подход к принятию решений. Этот метод позволяет нам визуализировать и взвесить различные аспекты наших решений перед тем, как принять окончательное решение.

Основная идея квадрата Декарта заключается в том, что мы разделяем наши решения на различные области, по которым они влияют на нашу жизнь, и оцениваем каждую область в соответствии с их важностью и приоритетами. Квадрат Декарта позволяет нам избежать субъективных предпочтений и принять обоснованное решение, основанное на наших уникальных потребностях и ценностях.

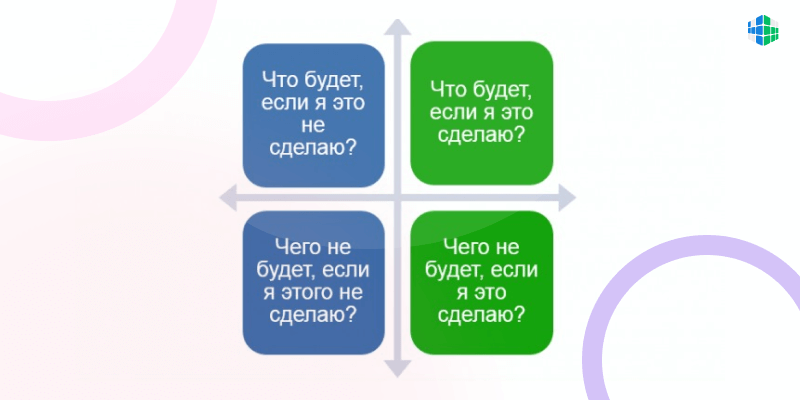
Квадрат Декарта состоит из четырех квадрантов, каждый из которых представляет определенную область принятия решений. Квадрант I представляет собой область высокой важности и высокого приоритета, квадрант II — низкой важности и высокого приоритета, квадрант III — низкой важности и низкого приоритета, а квадрант IV — высокой важности и низкого приоритета. Размещая наши решения в соответствующих квадрантах, мы можем легко определить, на что стоит сосредоточиться в первую очередь и что можно отложить на потом.

Использование квадрата Декарта для принятия решений является ценным инструментом не только в профессиональной сфере, но и в личной жизни. Он помогает нам взвесить все факторы и аспекты наших решений, чтобы избежать неправильных и необдуманных шагов. Следуя практическому руководству по использованию квадрата Декарта, мы можем повысить свою эффективность, снизить стресс и полностью осознать последствия своих решений.

Понимание квадрата Декарта

Квадрат Декарта — это графическое представление, которое помогает принимать решения и анализировать различные факторы. Этот инструмент предлагает систематический подход к оценке и визуализации данных, позволяя рассматривать их с разных точек зрения.

Основными компонентами квадрата Декарта являются оси x и y, которые представляют различные переменные и факторы. Ось x может представлять один аспект, а ось y — другой. В результате получается двумерный график, на котором каждая точка представляет конкретное значение переменных.

При использовании квадрата Декарта можно выявить зависимости и взаимосвязи между переменными. Значения осей могут быть пространственными, временными или другими факторами, в зависимости от того, что требуется анализировать.

Чтобы лучше понять график квадрата Декарта, полезно использовать дополнительные инструменты, такие как отметки, цветовая схема или разные символы для точек на графике. Это позволяет привнести дополнительную информацию и упростить интерпретацию данных.

Квадрат Декарта имеет широкий спектр применений. Он может использоваться в различных областях, таких как бизнес, наука, инженерия, медицина и другие. Этот инструмент помогает выявлять тренды, паттерны и аномалии, а также делать прогнозы и принимать обоснованные решения на основе анализа данных.

Определение и назначение квадрата Декарта

Квадрат Декарта — это графическое представление числовой системы, которое используется для принятия решений и анализа данных. Название «квадрат Декарта» происходит от французского математика и философа Рене Декарта, который разработал эту систему в 17 веке.

Одной из основных задач квадрата Декарта является систематизация информации и визуализация различных параметров для принятия обоснованных решений. Графическое представление данных позволяет увидеть связи и взаимосвязи между переменными и параметрами, а также идентифицировать тренды и паттерны, которые могут быть неочевидными при анализе их числовых значений.

Квадрат Декарта представляет собой декартову плоскость, в которой оси X и Y используются для отображения различных переменных или параметров. Ось X отображает одну переменную, а ось Y — другую переменную. Точки на графике представляют значения переменных и их соотношение.

Одна из особенностей квадрата Декарта заключается в том, что он может быть разделен на четверти, а также метками или областями, чтобы помочь в классификации и категоризации данных. Это позволяет улучшить понимание данных и лучше оценивать ситуацию при принятии решений на основе этих данных.

Таким образом, квадрат Декарта представляет собой мощный инструмент для анализа и принятия решений, который помогает структурировать и визуализировать данные, а также выявлять взаимосвязи и тренды, которые могут быть полезными при принятии обоснованных и информированных решений.

История и развитие квадрата Декарта

Квадрат Декарта, также известный как двумерная система координат, был разработан математиком и философом Рене Декартом в XVII веке. Это графический инструмент, который представляет собой плоскость, разделенную на две оси — горизонтальную (ось абсцисс) и вертикальную (ось ординат).

Идея квадрата Декарта возникла в процессе разработки Декартом алгебры и геометрии. Он осознал, что координаты точек на плоскости могут быть описаны числами и ввел систему численных значений для каждой оси. Это позволило ему представить геометрические фигуры и алгебраические уравнения в одной системе.

С течением времени квадрат Декарта стал неотъемлемой частью математики и нашел широкое применение в различных областях, включая физику, экономику и компьютерные науки. Он позволяет графически представлять данные, анализировать тенденции и принимать решения на основе визуальной информации.

С развитием технологий и появлением компьютеров квадрат Декарта стал еще более удобным и доступным. Появились специальные программы и инструменты, позволяющие создавать и редактировать графики, а также проводить сложные математические расчеты на основе данных, представленных в квадрате Декарта.

В настоящее время квадрат Декарта используется для решения самых разных задач — от построения графиков функций и изучения математических моделей до анализа производственных процессов и прогнозирования рыночных тенденций. Он позволяет наглядно отображать информацию и легко взаимодействовать с данными, что делает его ценным инструментом для принятия решений в различных сферах деятельности.

Ключевые понятия и принципы квадрата Декарта

Квадрат Декарта — это графический инструмент, который позволяет структурировать информацию и принимать решения на основе анализа различных факторов. Он представляет собой двумерное пространство, разделенное на четыре квадранта.

Первое ключевое понятие квадрата Декарта — это оси координат. Ось x представляет собой горизонтальную ось, на которой отображается один фактор или переменная, а ось y — вертикальную ось, представляющую другой фактор или переменную. Сочетание значений на обеих осях позволяет определить положение точки в квадрате Декарта.

Второе ключевое понятие — это четыре квадранта. Каждый квадрант имеет свою уникальную характеристику и репрезентирует определенную комбинацию значений на осях x и y. Например, верхний левый квадрант может представлять высокие значения на обеих осях, что указывает на положительное влияние двух факторов. В то же время, нижний правый квадрант может представлять низкие значения на обеих осях, что указывает на отрицательное влияние двух факторов.

Принцип квадрата Декарта заключается в том, чтобы использовать графическую репрезентацию данных на осях x и y для определения взаимосвязей между различными факторами или переменными и принятия рациональных решений. Квадрат Декарта позволяет визуализировать сложную информацию, помогает обнаружить тренды и паттерны, а также определить причинно-следственные связи между различными аспектами и проблемами.

Применение квадрата Декарта для принятия решений

Квадрат Декарта — это графическая методика, которая помогает систематизировать и анализировать информацию при принятии решений. Он представляет собой двумерную матрицу, где на одной оси отображаются факторы, влияющие на решение, а на другой оси — альтернативы для выбора.

Для использования квадрата Декарта необходимо определить список факторов, которые нужно учесть при принятии решения, и список возможных альтернатив. Затем каждой альтернативе и каждому фактору присваивается определенное значение на основе их важности и влияния на принятие решения.

Первый шаг: определить факторы и альтернативы. Например, если вы принимаете решение о выборе места для отдыха, факторами могут быть локация, климат, стоимость, доступность, качество услуг и т. д., а альтернативами — различные курорты или страны.

Второй шаг: задать значения каждой альтернативе и каждому фактору. Например, локация может быть оценена по шкале от 1 до 10, где 1 — очень плохо, а 10 — идеально. Таким образом, каждая альтернатива получит оценку по каждому фактору.

После того как все оценки заданы, можно начать заполнять квадрат Декарта, помещая альтернативы и факторы в соответствующие ячейки. Затем провести анализ полученной информации и выбрать наиболее подходящую альтернативу.

Преимущества использования квадрата Декарта:

• Позволяет систематизировать информацию и учесть все факторы, влияющие на принятие решения.
• Помогает визуализировать и сравнить различные альтернативы.
• Дает возможность объективно оценить каждую альтернативу и фактор.

Использование квадрата Декарта может значительно облегчить процесс принятия решения, особенно при сложных и многокритериальных задачах. Он помогает взвесить все факторы и выбрать наиболее оптимальное решение на основе объективной оценки.

Шаги процесса принятия решений с использованием квадрата Декарта

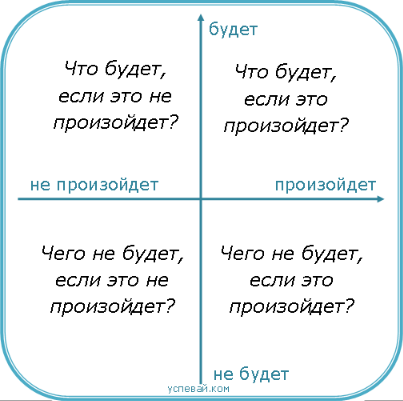
Процесс принятия решений с использованием квадрата Декарта представляет собой структурированный подход, который помогает принимать обоснованные и взвешенные решения. Вот несколько ключевых шагов, которые могут помочь вам использовать этот метод:

• Определить цель принятия решения. Прежде чем приступить к использованию квадрата Декарта, важно понять, какая цель стоит перед вами. Определите четко, какую проблему вы хотите решить или какой результат вы хотите достичь.
• Создать список факторов. Далее, составьте список факторов, которые могут влиять на ваше решение. Это могут быть различные критерии, такие как стоимость, время, качество, риск и т. д. Необходимо учесть все существенные факторы, которые могут оказать влияние на ваше принятие решения.
• Оценить каждый фактор. После составления списка факторов, следующий шаг — оценить каждый из них. Используйте шкалу оценки или числовые значения, чтобы выразить важность каждого фактора для вас.
• Построить квадрат Декарта. Теперь на основе оценки каждого фактора вы можете построить квадрат Декарта. Разделите квадрат на четыре части и поместите факторы в соответствующие квадранты в зависимости от их важности и воздействия на ваше решение.
• Проанализировать различные варианты решения. После построения квадрата Декарта, рассмотрите различные варианты решения и оцените их с помощью квадрата. Рассмотрите, как каждый из вариантов влияет на каждый фактор и как это соотносится с вашей целью.
• Выбрать оптимальное решение. Используя информацию из квадрата Декарта, выберите оптимальное решение, которое наилучшим образом соответствует вашей цели и удовлетворяет ваши потребности и предпочтения.

Применение квадрата Декарта позволяет структурировать процесс принятия решений, учитывая различные факторы влияния и оценивая их важность. Этот подход помогает принять обдуманное и информированное решение, основанное на весомых данных и ваших целях и приоритетах.

Примеры применения квадрата Декарта в различных сферах деятельности

Квадрат Декарта, также известный как «структурированный анализ принятия решений», является мощным инструментом, который может быть применен в различных сферах деятельности. Вот несколько примеров использования этого метода:

Менеджмент и бизнес

Квадрат Декарта может быть использован для анализа рисков и преимуществ при принятии стратегических решений в бизнесе. Он позволяет оценить внутренние и внешние факторы, влияющие на успех предприятия. Например, менеджер может использовать квадрат Декарта для определения, какие проекты следует приоритезировать, исходя из их потенциальной прибыльности и вероятности успеха.

Здравоохранение

В сфере здравоохранения квадрат Декарта может использоваться для принятия решений о лечении пациентов. Врачи могут оценить различные виды лечения и их потенциальные побочные эффекты, чтобы определить наиболее эффективный и безопасный подход к лечению. Кроме того, квадрат Декарта может быть полезен при определении приоритетов в области здравоохранения и распределении ресурсов.

Образование

В образовательной сфере квадрат Декарта может быть использован для определения приоритетов учебных программ, а также для выбора методов обучения. Педагоги могут оценивать достоинства и слабости различных подходов к обучению, чтобы определить наилучший способ передачи знаний и развития учеников. Квадрат Декарта также может помочь в определении задач, которые нужно решить, чтобы достичь образовательных целей.

Научные исследования

В научных исследованиях квадрат Декарта может использоваться для анализа данных, сравнения и оценки разных моделей или теорий. Используя этот метод, исследователи могут определить, какие факторы оказывают наиболее значимое влияние на исследуемую явление, и какие аспекты теории следует учесть при разработке дальнейших исследований.

Применение квадрата Декарта в различных сферах активности позволяет получить систематическую оценку, облегчает принятие информированных решений и способствует достижению поставленных целей.

Возможные проблемы и их решения при использовании квадрата Декарта

Использование квадрата Декарта для принятия решений может столкнуться с рядом возможных проблем. Одной из них является несоответствие между затраченными усилиями и достигнутыми результатами. Возможно, вы потратили много времени и ресурсов на выполнение определенной задачи, но в итоге получили незначительный или неудовлетворительный результат. В такой ситуации решением может быть пересмотр и корректировка стратегии действий, а также более тщательное оценивание потенциальных результатов.

Еще одной возможной проблемой при использовании квадрата Декарта является неполнота или некорректность информации, на основе которой принимается решение. Неправильное восприятие фактов или недостаток объективной информации может привести к неправильному выбору стратегии или решения. В таких случаях рекомендуется провести более тщательную оценку информации, использовать дополнительные источники и привлечь экспертов для получения более полной и достоверной информации.

Также возможной проблемой является неправильная оценка важности и приоритетности факторов, влияющих на принятие решения. В квадрате Декарта значения осей представляют важность и эффективность различных факторов или альтернатив. Однако, при неправильной оценке значимости этих факторов и альтернатив, принятое решение может быть нерациональным и неэффективным. Решением этой проблемы может быть более тщательная и объективная оценка значимости каждого фактора и альтернативы, а также проведение анализа чувствительности для определения наиболее важных переменных.

Еще одной проблемой при использовании квадрата Декарта может быть недостаточное вовлечение всех заинтересованных сторон в принятие решения. Если важные заинтересованные стороны не участвуют в процессе принятия решения или их мнение не учитывается, это может привести к недовольству, конфликтам и неэффективным результатам. Решением данной проблемы может быть более широкое вовлечение и консультация всех заинтересованных сторон, проведение совместных обсуждений и поиск компромиссных решений.

Преимущества и ограничения квадрата Декарта

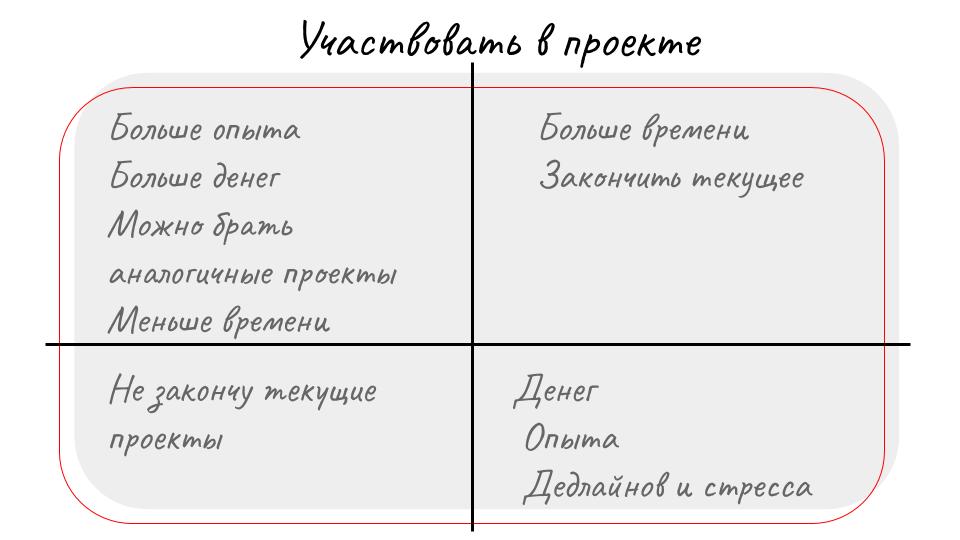
Квадрат Декарта – это графическое представление данных, использующее оси абсцисс и ординат для размещения информации. У него есть ряд преимуществ, которые делают его полезным инструментом в принятии решений.

Одним из главных преимуществ квадрата Декарта является его простота в использовании. Пользователю не требуется специальных навыков или знаний для того, чтобы построить такую диаграмму и анализировать данные. Это делает его доступным и полезным инструментом для широкого круга пользователей.

Квадрат Декарта позволяет визуализировать данные и отобразить связи между ними. Он позволяет легко сравнивать и анализировать значения на основе их положения на графике. Это особенно полезно, когда нужно принять решение на основе большого количества информации и взаимосвязей между ней.

Однако, у квадрата Декарта есть и определенные ограничения. Во-первых, он может быть неэффективным, если данные имеют сложную структуру или нелинейные связи. В таких случаях может потребоваться использование других инструментов для анализа данных.

Также квадрат Декарта может не быть подходящим для визуализации больших объемов данных. Если количество данных слишком велико, то график может стать загроможденным и трудночитаемым. В таких случаях может быть полезным использование расширенных инструментов для визуализации данных.

Несмотря на ограничения, квадрат Декарта остается широко используемым инструментом в принятии решений. Его преимущества в простоте использования и возможности визуализации данных делают его ценным инструментом для анализа информации и принятия важных решений.

Основные преимущества использования квадрата Декарта

Квадрат Декарта — это графический инструмент, который позволяет анализировать и принимать решения на основе двух взаимосвязанных переменных. Использование квадрата Декарта имеет ряд преимуществ, которые делают его полезным инструментом в различных областях.

Во-первых, квадрат Декарта позволяет наглядно отобразить информацию и визуализировать связь между двумя переменными. Это делает его отличным средством для проведения анализа и исследования данных. Благодаря квадрату Декарта становится понятно, как влияет одна переменная на другую, и можно выявить закономерности и тренды.

Во-вторых, квадрат Декарта помогает оценить важность каждой переменной и определить их приоритеты. Используя двухмерную графику, можно увидеть, как каждая переменная влияет на конечный результат. Это позволяет принять обоснованное решение и сфокусироваться на наиболее значимых переменных.

Кроме того, квадрат Декарта облегчает прогнозирование и планирование. Анализируя данные и представляя их в виде графика, можно увидеть, как изменение одной переменной будет влиять на другую. Это помогает прогнозировать будущие события и принимать решения, основанные на существующих тенденциях.

Наконец, квадрат Декарта позволяет принимать обоснованные решения на основе данных, а не на интуиции или случайности. Анализируя взаимосвязь двух переменных и их влияние на определенный итог, можно принять решение, основанное на фактах и логике.

В целом, использование квадрата Декарта представляет собой мощный аналитический и решающий инструмент, который позволяет наглядно отобразить информацию, определить приоритеты, прогнозировать и принимать обоснованные решения на основе данных.

Ограничения и возможные альтернативы квадрату Декарта

Хотя квадрат Декарта может быть полезным инструментом для принятия решений, он также имеет свои ограничения. Во-первых, это ограничение в отношении количества переменных, которые можно учесть в процессе принятия решения. Квадрат Декарта идеально подходит для решения простых задач с двумя переменными, но становится менее эффективным при увеличении их числа.

Кроме того, квадрат Декарта не учитывает взаимодействие переменных между собой. Он разбивает пространство принятия решений на независимые области, предполагая, что изменение одной переменной не влияет на другую. Однако в реальности переменные могут быть взаимосвязаны, и это может привести к неправильным выводам.

Существуют альтернативы квадрату Декарта, которые могут помочь в преодолении этих ограничений. Одной из таких альтернатив является метод анализа иерархий (МАИ), который позволяет учитывать взаимосвязь между переменными и оценивать их относительную важность. Другой альтернативой может быть использование статистических методов, таких как регрессионный анализ или методы машинного обучения, которые могут учитывать сложные взаимосвязи между переменными и предсказывать результаты на основе имеющихся данных.

В конечном счете, выбор метода для принятия решений зависит от конкретных задач и доступных данных. Возможно, комбинация различных методов и анализов может быть наиболее эффективной стратегией, позволяющей учесть как отдельные переменные, так и их взаимосвязи. Независимо от выбора, важно учитывать ограничения и преимущества каждого метода, чтобы принять наиболее информированное решение.