Как решить задачу со спичками: подробное объяснение

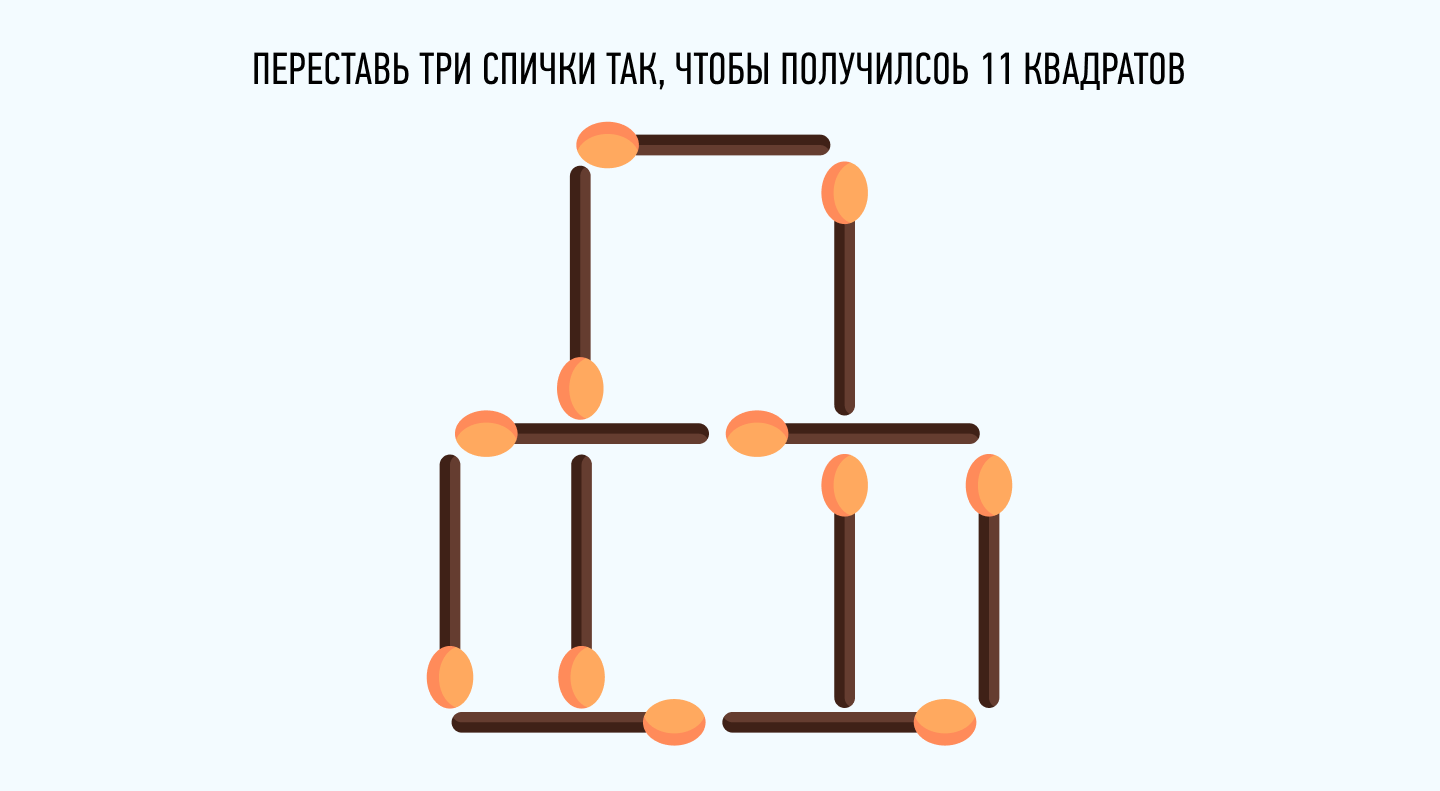
Задачи со спичками – классические головоломки, которые требуют творческого и логического мышления для их решения. Они часто используются в учебных заведениях и различных интеллектуальных играх. В данной статье мы рассмотрим процесс решения задачи со спичками на примере одной из наиболее популярных головоломок – задачи о перестановке спичек.

Головоломка состоит из группы спичек, расположенных в определенной фигуре или шаблоне. Задача заключается в том, чтобы переставить определенное количество спичек для того, чтобы получить новую фигуру или шаблон. Ограничения на количество переставляемых спичек и способ их перестановки могут варьироваться, что делает задачу по-настоящему интересной и разнообразной.

Решение задачи со спичками требует тщательного анализа и логического рассуждения. Важно учитывать каждое действие и предугадывать его последствия. Часто приходится пробовать различные варианты и искать нестандартные решения. Тем не менее, с практикой и развитием мышления задачи со спичками становятся все более доступными и интересными.

Первый шаг: набор со спичек

Первым шагом в решении задачи со спичками является формирование набора из необходимого количества спичек. В каждой конкретной задаче указывается, сколько спичек доступно и как их можно использовать. Необходимо внимательно прочитать условие задачи и определить, какие правила регулируют использование спичек.

Для удобства решения задачи, полезно представить набор спичек в виде таблицы или списка. Таблица может включать две колонки, где в одной указывается номер спички, а во второй — ее состояние (например, «горит», «не горит»). Список можно оформить, используя маркированный или нумерованный список.

Важно правильно настроить набор спичек, чтобы соответствовать требованиям задачи. Например, если в задаче указано, что можно использовать только определенное количество спичек, то необходимо правильно выбрать их, чтобы не превысить лимит.

При решении задачи со спичками важно оставаться внимательным и аккуратным при создании набора. Каждая спичка может оказаться ключевой для решения, поэтому нельзя упустить даже малозначимые детали. В процессе выполнения задачи необходимо использовать логическое мышление и умение анализировать информацию, чтобы правильно подходить к формированию набора со спичками.

Принципы соблюдения

Для эффективного решения задачи со спичками необходимо придерживаться нескольких принципов:

1. Анализировать условие задачи: Важно тщательно прочитать и понять условие задачи. Необходимо определить цель задачи, выделить все известные факты и условия, а также выяснить, какие параметры можно изменять.

2. Структурировать информацию: После анализа условия задачи следует структурировать всю доступную информацию. Это позволит лучше организовать мысли и представить задачу в понятном виде.

3. Использовать систематический подход: Для решения задачи со спичками необходимо использовать систематический подход, разбивая ее на более простые части и рассматривая различные варианты решений. Важно проводить логические операции и обращать внимание на детали.

4. Проводить проверку: После получения решения задачи со спичками необходимо провести проверку, чтобы убедиться в его правильности. Для этого можно использовать рассуждения и логические рассуждения, а также предположить возможные варианты и проверить их с использованием условий задачи.

5. Работать с учетом ограничений: Важно учитывать возможные ограничения при решении задачи со спичками. Например, максимальное количество доступных спичек или определенные правила, которые необходимо соблюдать. Такие ограничения могут оказывать существенное влияние на выбор решения или его эффективность.

Соблюдение данных принципов поможет справиться с задачей со спичками и достичь желаемого результата. Важно быть терпеливым, творческим и готовым к нестандартным решениям.

Выбор вершины для набора со спичками

При решении задачи со спичками важно правильно выбрать вершину, с которой начать набор. В зависимости от выбранной вершины может меняться стратегия решения и итоговый результат. В этом абзаце мы рассмотрим несколько способов выбора вершины для набора со спичками.

1. Самая длинная вершина: Если в задаче имеется вершина, состоящая из наибольшего количества спичек, ее можно выбрать в качестве стартовой. В этом случае, при решении задачи, возможно использование наибольшего количества спичек и получение наиболее крупного итогового результата.

2. Самая короткая вершина: Возможен также вариант выбора самой короткой вершины в качестве стартовой. В этом случае, при решении задачи, можно быстро использовать некоторое количество спичек и уменьшить общее количество требуемых шагов.

3. Стратегия поиска: Еще одним подходом является использование стратегии поиска, например, глубинного или широкого поиска. При глубинном поиске выбирается ближайшая вершина соединенная с текущей. При широком поиске выбираются все вершины, соединенные с текущей, и одна из них выбирается в качестве стартовой.

В конечном счете, выбор вершины для набора со спичками зависит от условий задачи и особенностей решения. Важно анализировать имеющиеся данные и применять подходящую стратегию, чтобы достичь наилучшего итогового результата.

Проверка на количество спичек

При решении задачи со спичками важно учитывать количество доступных спичек, чтобы их использование было оптимальным и не приводило к излишнему или недостаточному количеству спичек. Для этого следует продумать стратегию и анализировать ситуацию.

Проверка на количество спичек является важным этапом решения задачи. Необходимо убедиться, что количество доступных спичек соответствует условиям задачи. Для этого можно воспользоваться счетчиком или отдельным переменным, которые будут отслеживать использование спичек и их остаток.

Если в условии задачи указано, что единовременно можно использовать определенное число спичек, нужно проверить, что это число меньше или равно общему количеству спичек. В противном случае решение задачи невозможно.

Также, при проверке на количество спичек, необходимо учитывать возможность использования спичек несколько раз. В этом случае стоит проверить, что общее количество использованных спичек не превышает количество доступных. Иначе, нужно пересмотреть стратегию решения и найти другой подход.

В итоге, проверка на количество спичек является важным этапом решения задачи со спичками. Она позволяет убедиться, что выбранная стратегия выполнима и не нарушает условия задачи. Такой подход помогает сохранить оптимальное использование спичек и получить правильный результат.

Решение необходимости добавления новых спичек

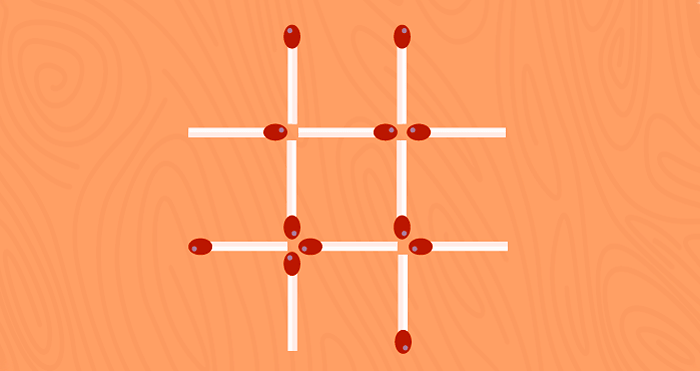
Когда решение задачи со спичками стало представляться невозможным с использованием имеющегося количества спичек, необходимо искать варианты добавления новых. Однако, перед тем как прибегать к этому, стоит убедиться в том, что все возможные комбинации существующих спичек уже были исследованы и не дали решения.

Чтобы определить, сколько дополнительных спичек нужно добавить, необходимо проанализировать условия задачи и провести соответствующие вычисления. Иногда для нахождения оптимального количества дополнительных спичек приходится использовать математические методы и алгоритмы.

Варианты добавления новых спичек могут быть разнообразными. Одним из подходов может быть привлечение дополнительных спичек из других источников. Например, можно попросить товарищей или знакомых предоставить необходимое количество спичек. Также возможно приобретение нужного количества спичек в магазине или заказ через интернет.

Необходимо также учитывать, что добавление новых спичек может изменить условие задачи и требовать пересмотра решения. Возможно, потребуется применение других логических или математических методов для достижения поставленной цели.

Как набирать со спичками

Игра со спичками – это увлекательная головоломка, которая требует логического мышления и терпения. Чтобы набрать какое-либо число с помощью спичек, необходимо использовать свою фантазию и креативный подход. Ниже представлены несколько способов, как можно набрать число со спичками.

1. Примерное равенство

Один из способов – использовать спички, чтобы создать символ или цифру, похожую на нужное число. Например, для набора числа 7 можно сделать семерку из спичек или используйте фантазию, чтобы создать нечто похожее на это число.

2. Комбинирование

Другой способ – комбинировать спички, чтобы образовать нужное число. Например, чтобы набрать число 9, можно взять одну спичку для создания цифры 1 и две спички для создания цифры 8, затем разместите их рядом друг с другом.

3. Арифметика

Также можно использовать арифметические операции, чтобы набрать нужное число с помощью спичек. Например, если вы хотите набрать число 5, возьмите 4 спички и сложите их вместе, затем добавьте еще одну спичку, чтобы получить 5.

4. Другие символы

Иногда можно использовать другие символы, чтобы представить нужное число. Например, чтобы набрать число 0, можно сделать круглый символ с помощью спичек.

5. Комбинаторика

Воспользуйтесь комбинаторикой, чтобы набрать число с помощью спичек. Например, можно построить таблицу, в которой каждая ячейка имеет определенную весовую ценность, и сложить вместе ячейки, чтобы получить нужное число.

Правила использования спичек

Правила использования спичек должны быть соблюдены строго, чтобы избежать возможных проблем и опасных ситуаций. Вот основные правила, которые следует учитывать при использовании спичек:

1. Не используйте спички в близкой близости к легковоспламеняющимся материалам. Спички могут вызвать пожар или даже взрыв, если они поджечены рядом с легковоспламеняющимися материалами, такими как спирт, газ или лак.
2. Не играйте спичками и не бросайте их на проходимую часть или в другие люди. Это может привести к серьезным травмам или пожарам.
3. Не пытайтесь поджечь неодинаковыми спичками одну и ту же подружку. Это может привести к несовместимости спичек или неожиданному воспламенению, что может быть опасно.

Дополнительно, следует помнить о том, что спички содержат скользящую или горящую головку, и могут вызывать ожоги при неправильном обращении с ними. Необходимо соблюдать все предосторожности при работе со спичками, включая держание их вдали от детей и хранение их в специальных контейнерах. Обязательно следите за своей безопасностью и не забывайте о правилах пожарной безопасности.

Выбор стратегии набора

При решении задачи со спичками важно выбрать правильную стратегию набора для достижения желаемого результата. От выбора стратегии будет зависеть сложность и время, необходимое для решения задачи.

Одна из стратегий набора — это пошаговое решение, при котором рассматриваются возможные варианты на каждом шаге и выбираются наиболее подходящие. При этом необходимо анализировать все возможные ходы и прогнозировать их последствия.

Другая стратегия набора — это разделение задачи на более простые подзадачи. В этом случае решение задачи со спичками может быть разбито на несколько меньших задач, которые легче решить по отдельности. Затем полученные решения можно объединить для получения финального результата.

Также можно использовать стратегию исключения, при которой анализируются все возможные ходы и исключаются такие, которые приводят к нежелательному результату. Эта стратегия позволяет эффективно уменьшить количество вариантов и сосредоточиться на наиболее перспективных ходах.

Проверка стабильности набора

Проверка стабильности набора спичек в задаче осуществляется путем анализа возможных изменений, которые можно сделать с данным набором. Для этого нужно проверить, может ли выполниться какое-либо действие с набором спичек таким образом, чтобы его структура изменилась или число спичек в наборе увеличилось или уменьшилось.

Одним из способов проверки стабильности набора является определение количества спичек в каждой группе. Если в каждой группе имеется одинаковое количество спичек, то можно считать, что набор является стабильным. Если же количество спичек в группах отличается, то набор не является стабильным.

Еще одним способом проверки стабильности набора спичек является анализ возможных действий с ним. Если при изменении расположения или удалении одной или нескольких спичек возможно получить новый набор, то исходный набор не является стабильным. Если же ни при одном из таких действий невозможно получить новый набор, то его можно считать стабильным.

Второй шаг: решение задачи

Чтобы решить задачу со спичками, необходимо продолжить размышление, которое было начато на первом шаге. Нужно уяснить, какие действия можно выполнить с данным количеством спичек и какие результаты они могут дать.

На этом шаге начинается процесс поиска решения задачи. Он может быть достаточно сложным и требовать терпения и логического мышления. Но не стоит отчаиваться, так как все задачи со спичками имеют решение.

Для того чтобы облегчить процесс решения, полезно составить таблицу, где будут перечислены все возможные комбинации действий и их результаты. Такая таблица поможет систематизировать информацию и увидеть закономерности.

Кроме того, стоит обратить внимание на особенности задачи. Например, если задача предполагает, что спички можно переломлять или складывать, то это открывает дополнительные возможности для нахождения решения.

По мере продвижения в решении задачи, стоит отмечать уже примененные действия и их результаты. Так будет легче отслеживать прогресс и не затеряться в уже проверенных вариантах.

Важно помнить, что решение задачи может потребовать не только логического мышления, но и интуиции. Sледует доверять своим интуитивным ощущениям и не бояться пробовать различные варианты. Часто, неожиданное решение может оказаться самым правильным.

Образование цифр

В процессе образования цифр у детей имеется несколько этапов. Первоначально дети начинают узнавать цифры и называть их по порядку: один, два, три и так далее. На этом этапе важно показывать детям изображения цифр и повторять их названия, чтобы они научились распознавать эти символы.

После этого дети начинают осознавать количество предметов, соответствующее каждой цифре. Например, они узнают, что цифра «два» означает два предмета, цифра «три» — три предмета и так далее. Для закрепления этого знания можно использовать специальные материалы, например, наборы с цифрами и предметами для счета.

Затем дети начинают учиться записывать цифры. На этом этапе они узнают форму и направление письма каждой цифры. Важно обучать детей правильно держать карандаш и следовать по контуру цифры, чтобы они научились писать ее правильно.

После того как дети научились записывать цифры, они учатся складывать и вычитать с их помощью. Здесь также используется визуализация, например, раскладывание спичек или предметов по цифрам для иллюстрации суммы или разности.

В заключение, образование цифр включает узнавание и название цифр, осознание количества, запись цифр и использование их для математических операций. Важно заниматься образованием цифр в игровой форме, используя визуализацию и практические задания, чтобы дети лучше запоминали и усваивали это знание.

Расположение спичек для формирования цифры

Расположение спичек может быть использовано для формирования различных цифр. Однако, для каждой цифры это расположение уникально и требует внимательного подхода.

Для формирования цифры 0 можно использовать три горизонтальные спички, размещенные друг под другом. Такое расположение подчеркивает форму цифры и делает ее легко узнаваемой.

Цифра 1 формируется с помощью двух спичек, которые располагаются вертикально. Одна из спичек служит основанием, а вторая примыкает к ней почти под прямым углом.

Для создания цифры 2 нужно использовать пять спичек. Три спички располагаются горизонтально под углом к основанию, а две вертикальные спички упираются в них, образуя угол.

Цифра 3 создается с использованием пяти спичек. Три вертикальные спички располагаются под углом к основанию, а две горизонтальные спички примыкают к ним, образуя угол.

Цифра 4 формируется с помощью четырех спичек. Две горизонтальные спички располагаются на основании, а остальные две вертикальные спички примыкают к основанию и пересекаются вверху.

Цифра 5 создается с помощью пяти спичек. Две вертикальные спички располагаются на основании, а третья спичка идет по диагонали от одной вертикальной спички к другой. Две горизонтальные спички примыкают к вертикальным спичкам на определенном расстоянии.

Для формирования цифры 6 нужно использовать пять спичек. Две вертикальные спички располагаются на основании, а третья спичка идет по диагонали от одной вертикальной спички к другой. Остальные две спички примыкают к нее справа и слева на небольшом расстоянии.

Анализ различных вариантов составления цифр

Задача со спичками на составление цифр может иметь множество вариантов решения, каждый из которых требует логического мышления и творческого подхода. В данном анализе рассмотрим несколько возможных вариантов составления цифр с использованием спичек.

Для создания цифр можно использовать как стандартные, так и нестандартные формы, комбинировать несколько спичек в одну цифру или использовать их отдельно. При этом важно учитывать, что каждая цифра имеет свою уникальную структуру и требует определенных пропорций.

Одним из самых простых вариантов составления цифр является использование спичек в форме горизонтальных или вертикальных линий. Например, цифру «1» можно представить одной вертикальной спичкой, а цифру «7» — горизонтальной спичкой с еще одной спичкой, выступающей в сторону.

Однако, существуют и более сложные варианты составления цифр. Например, цифру «2» можно представить с помощью двух горизонтальных спичек, пересекающихся в середине, или с использованием одной вертикальной спички с двумя горизонтальными спичками, идущими книзу и влево.

Для создания цифр «3» и «8» также можно использовать комбинацию горизонтальных и вертикальных спичек, но уже с другими пропорциями и углами. Для цифры «3» можно использовать две горизонтальные спички, образующие своеобразную угловатую форму, а для цифры «8» — две круглые горизонтальные спички, пересекающиеся в центре.

Существует также принцип использования отдельных спичек для создания цифр, например, цифра «4» может быть собрана из трех горизонтальных спичек, а цифра «9» — из одной горизонтальной и одной вертикальной спички.

В целом, анализируя различные варианты составления цифр с помощью спичек, видно, что существует множество возможностей и вариантов творческого подхода. Каждый вариант требует от пользователя аналитических и логических навыков, а также способности видеть уникальные формы и структуры в представлении цифр.

Проверка правильности образования цифры

При решении задачи со спичками, одним из ключевых моментов является проверка правильности образования цифры. Всего существует 10 цифр — от 0 до 9, и каждая из них должна быть собрана из определенного количества спичек. Для проверки правильности образования цифры нужно учесть, сколько спичек требуется для ее создания.

Образование цифры 0 требует использования 6 спичек, при этом они должны быть расположены в форме прямой горизонтальной линии. Отсутствие спичек в определенных местах или их добавление может привести к неправильному образованию цифры.

Цифра 1 состоит из 2 спичек — одной вертикальной и одной горизонтальной. Если спички расположены неправильно или добавлены лишние, образование цифры будет некорректным.

Цифра 2 формируется из 5 спичек, которые располагаются так, чтобы образовать контур цифры. Любые нарушения этой формы свидетельствуют о неправильном образовании цифры.

Проверка правильности образования цифры 3 включает в себя наличие 5 спичек, расположенных в определенном образе, который символизирует цифру.

Цифра 4 образуется из 4 спичек — 3 вертикальных и 1 горизонтальной. При создании этой цифры необходимо учесть правильное расположение спичек, иначе цифра будет сформирована неправильно.

Образование цифры 5 требует использования 5 спичек в определенной последовательности. Необходимо проверить правильность расположения каждой спички для создания правильной цифры.

Цифра 6 образуется из 6 спичек, их расположение должно образовывать спираль. Любое отклонение от этого образца свидетельствует о неправильном образовании цифры.

Проверка правильности образования цифры 7 включает в себя наличие 3 спичек, которые должны быть расположены в соответствии с формой этой цифры.

Цифра 8 формируется из 7 спичек, расположенных таким образом, чтобы создать контур цифры. Неправильное образование этой цифры будет иметь другую форму, отличную от ожидаемой.

Цифра 9 образуется из 6 спичек, их расположение должно образовывать контур цифры. Любое отклонение от этой формы свидетельствует о неправильном образовании цифры.

Использование арифметических действий

Для решения задачи со спичками можно использовать арифметические действия, чтобы сгруппировать и перемещать спички. Это поможет нам создавать различные фигуры и решать сложные головоломки.

Например, если у нас есть задача с подписью «переместите одну спичку, чтобы получить правильное математическое равенство», мы можем использовать арифметические операции, такие как сложение, вычитание, умножение и деление, чтобы изменить расположение спичек и получить верное равенство.

Также можно использовать арифметические операции для создания математических фигур со спичками. Например, с помощью сложения и вычитания можно создать треугольник, квадрат или ромб. Умножение и деление могут использоваться для создания более сложных фигур, таких как пентагон или звезда.

Использование арифметических действий в решении задач со спичками требует сочетания логического мышления, математических навыков и креативных подходов. Оно позволяет нам развивать наше воображение, а также улучшать наши навыки решения проблем и анализа.

Способы использования спичек для арифметических действий

Спички могут оказаться полезным инструментом для выполнения арифметических действий в нестандартных ситуациях. С использованием спичек можно проводить операции сложения, вычитания, умножения и деления, представляя числа и символы с помощью палочек.

Например, для сложения двух чисел можно использовать спички для представления цифр и проводить соответствующие операции сложения. Каждая спичка может обозначать единицу, и, соединяя их вместе, можно получить сумму.

Для вычитания можно использовать спички для представления чисел и провести операцию вычитания, удаляя или перераспределяя спички по разрядам. Например, чтобы вычесть одно число из другого, можно удалять спички, соответствующие определенным разрядам, чтобы получить результат.

Для умножения можно использовать спички для представления чисел и провести операцию умножения, соединяя их способом, в котором каждая спичка обозначает определенное число. Например, можно соединить спички в форме прямоугольника или ромба для обозначения произведения чисел.

Для деления можно использовать спички для представления чисел и провести операцию деления, разделяя спички между группами с помощью дополнительных спичек. Например, можно разделить одну группу спичек на равные части, чтобы получить результат деления.

Таким образом, спички можно использовать для выполнения различных арифметических действий, представляя числа и символы с помощью палочек и проводя соответствующие операции.

Определение порядка применения арифметических действий

Порядок применения арифметических действий определяет последовательность выполнения математических операций. Это необходимо, чтобы получить правильный результат вычислений.

В математике существует определенный порядок, в котором выполняются арифметические операции. Сначала выполняются операции в скобках, затем возведение в степень, умножение и деление, и, наконец, сложение и вычитание.

Если в выражении присутствуют скобки, то сначала выполняются операции внутри скобок, начиная с самых внутренних скобок и двигаясь к внешним. При этом, если внутри скобок есть еще скобки, в них надо также выполнить операции по этому же правилу.

Далее, если в выражении присутствует возведение в степень, то это действие выполняется после операций в скобках. Затем выполняются операции умножения и деления, по порядку слева направо.

Наконец, после выполнения всех операций в скобках, возведения в степень, умножения и деления, последними выполняются операции сложения и вычитания.

Чтобы избежать ошибок и получить правильный результат, важно следовать порядку применения арифметических действий и явно указывать скобки для уточнения приоритета операций.

Проверка корректности решения задачи

После того как вы решите задачу со спичками, необходимо провести ее проверку, чтобы убедиться в корректности выбранного решения. Во-первых, нужно убедиться, что вы соблюдаете правила задачи, а именно: использовать оговоренное количество спичек и соблюдать условия и ограничения, заданные в тексте задачи.

Для проверки корректности решения задачи можно использовать различные методы. Один из них — самостоятельная проверка. В этом случае следует перечислить все действия, которые вы выполнили со спичками, и сравнить результат с требуемым. Также можно прогнать решение через несколько тестовых сценариев, чтобы убедиться, что оно работает правильно в различных случаях.

Также можно использовать математические методы для проверки корректности решения задачи со спичками. Проверьте, что полученный результат соответствует заявленному условию задачи. Для этого можно воспользоваться алгеброй, геометрией или другими математическими методами в зависимости от конкретной задачи.

Наконец, проверку корректности решения может проводить другой человек. Предложите свое решение задачи со спичками кому-то другому и попросите его проверить его на правильность. Другой человек может заметить ошибки или недочеты, которые вы упустили. Не забывайте, что взгляд со стороны может быть очень полезен при проверке решения задачи.

Третий шаг: анализ и оптимизация

Анализ: на данном этапе следует проанализировать все шаги, выполненные в предыдущих этапах, и оценить их эффективность. Необходимо выявить, какие из них привели к верным решениям, а какие были неоптимальными или ошибочными.

Во время анализа нужно обратить внимание на логику своих решений и поискать возможность оптимизации. Может быть, есть более эффективный алгоритм или подход к решению задачи со спичками. Необходимо также проверить корректность всех решений и убедиться, что они соответствуют условию задачи.

Если в процессе анализа вы обнаружили ошибку, необходимо вернуться к предыдущим шагам и внести корректировки. Также можно провести дополнительные эксперименты или тесты, чтобы убедиться в правильности решения задачи.

Оптимизация: после проведения анализа можно перейти к оптимизации решения. Здесь следует искать способы улучшить эффективность алгоритма или сократить количество шагов для достижения результата.

Один из подходов к оптимизации – это поиск общих паттернов или закономерностей, которые повторяются в разных задачах со спичками. Использование этих шаблонов может значительно упростить решение задачи и сократить количество необходимых действий.

Следует также обратить внимание на возможные оптимизации, связанные с минимизацией числа спичек, максимальным использованием каждой из них или улучшением алгоритма поиска решения.

Поиск лучшего решения

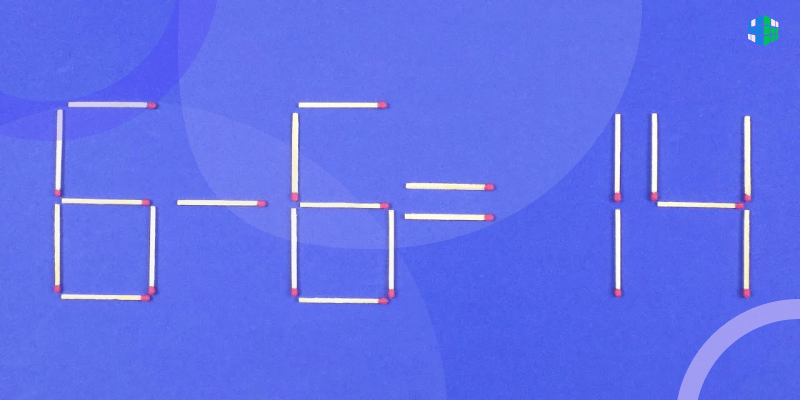
Решение задачи со спичками требует тщательного анализа и поиска наилучшего варианта. Для этого можно применить различные стратегии и методы.

Первым шагом в поиске лучшего решения является изучение условий задачи и понимание ограничений. Необходимо определить, сколько спичек доступно, какие операции можно выполнять с ними и какое конечное условие нужно достичь.

Затем следует провести анализ возможных вариантов решения и оценить их эффективность. Можно использовать таблицу для визуализации всех возможных сочетаний операций и их результатов.

Критерии оценки эффективности решения могут включать количество использованных спичек, количество операций, время выполнения и конечное состояние системы спичек.

Для поиска лучшего решения также полезно применять методы моделирования и симуляции. Они позволяют провести эксперименты на компьютере и оценить различные варианты решения без необходимости выполнения операций со спичками в реальности.

В итоге, поиск лучшего решения задачи со спичками требует систематического и аналитического подхода. Он предполагает изучение условий задачи, анализ возможных вариантов решения, оценку их эффективности и применение методов моделирования. Только таким образом можно найти оптимальное решение этой задачи.

Анализ различных вариантов решения задачи

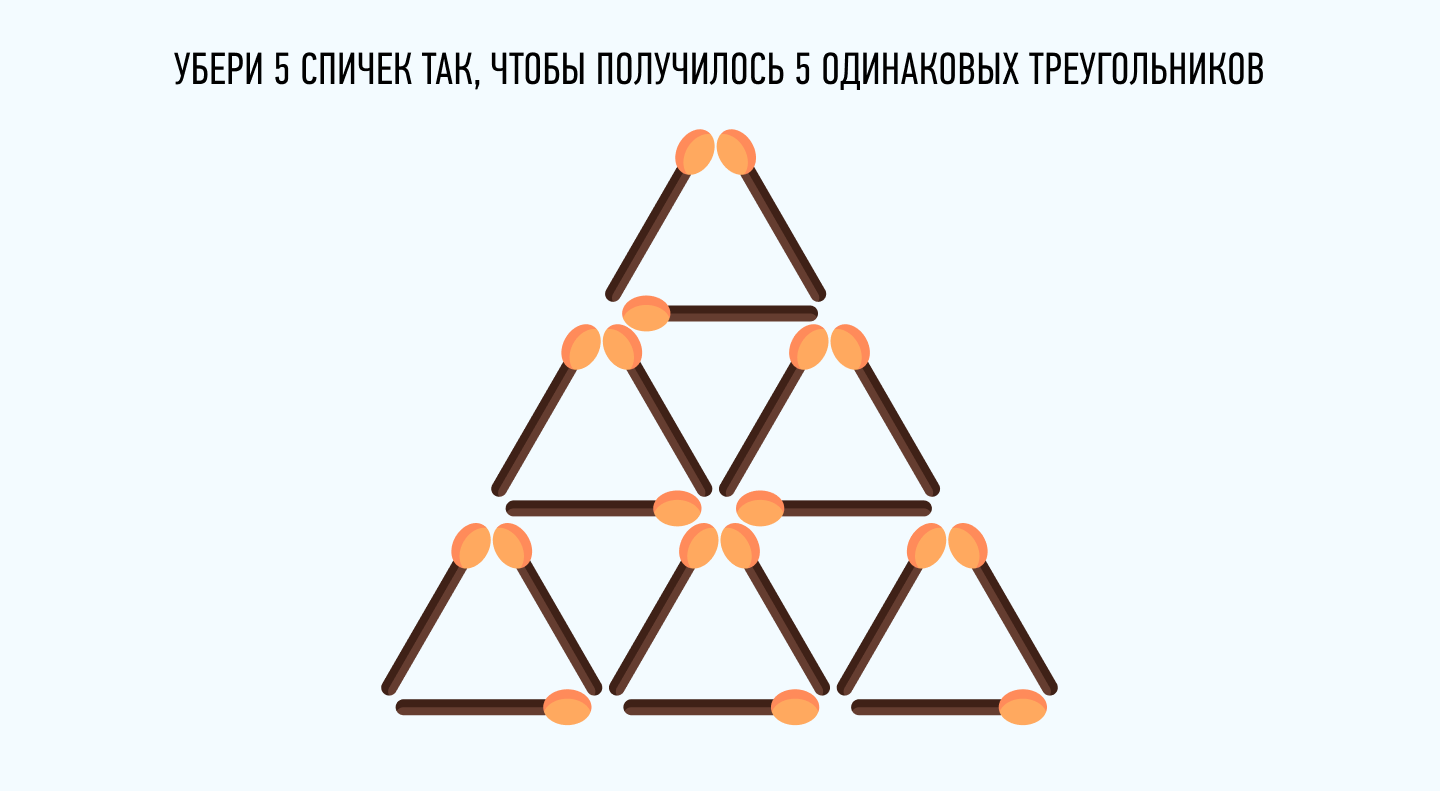
Задача со спичками — это классическая математическая головоломка, которая требует логики и творческого подхода для решения. Существует несколько различных вариантов решения этой задачи, каждый из которых имеет свои особенности и предпочтительные условия применения.

Первым вариантом решения может быть использование простых арифметических операций и сравнений для нахождения решения. Наличие математической подготовки позволит систематизировать информацию и применить формулы для получения ответа. Этот метод наиболее подходит для задач, в которых есть точные условия и известные ограничения.

Второй вариант решения может состоять в использовании графического представления задачи. Это может быть требуется, когда условия задачи необходимо визуализировать, чтобы иметь более ясное понимание и лучшую ориентировку по решению. Использование диаграмм, графиков или таблиц может помочь в структурировании информации и обнаружении различных сценариев решения.

Третий вариант решения связан с использованием рекурсии и алгоритмов. В этом случае задача может быть разбита на более мелкие подзадачи, которые решаются по отдельности. Затем полученные результаты комбинируются для получения окончательного решения. Этот метод подходит для сложных задач, где необходимо рассмотреть множество возможных вариантов и учитывать разные условия.

Каждый из этих вариантов решения имеет свои преимущества и недостатки, и, в зависимости от условий задачи и личных предпочтений, можно выбрать оптимальный подход для ее решения. Важно учитывать свои сильные стороны и использовать метод, который наиболее эффективно поможет найти правильное решение задачи со спичками.

Определение оптимального количества спичек

Когда мы решаем задачу со спичками, одним из важных аспектов является определение оптимального количества спичек для достижения желаемого результата. Необходимо продумать стратегию и выбрать наиболее эффективное количество спичек.

При решении задачи со спичками, целью может быть как получение определенного результата (например, создание определенной фигуры), так и определение минимального количества ходов для достижения этого результата.

Чтобы определить оптимальное количество спичек, нужно анализировать состояние исходной конфигурации, вычислять возможные варианты ходов и их последствия, а также учитывать ограничения и условия задачи.

Можно применять различные стратегии и методы, например, пробовать разные варианты ходов и оценивать их эффективность, использовать методы перебора или оптимизации, анализировать ситуацию на каждом ходу и принимать решение на основе этого анализа.

Определение оптимального количества спичек является важным шагом в решении задачи со спичками. Благодаря правильно выбранной стратегии и количеству спичек, можно достичь требуемого результата с минимальными затратами времени и усилий.

Улучшение времени выполнения

Для улучшения времени выполнения задачи со спичками можно использовать различные стратегии и оптимизации.

Во-первых, можно сократить количество операций, проводимых с каждой партией спичек. Например, можно уменьшить количество «сжиганий» спичек, заменяя их комбинациями из более маленьких партий. Это позволит более эффективно использовать спички и сократить время на каждую операцию.

Во-вторых, можно использовать алгоритмы и структуры данных, которые позволят выполнять задачу быстрее. Например, можно использовать алгоритмы динамического программирования или алгоритмы с ветвлением и ограничениями. Такие алгоритмы позволяют находить оптимальные решения и исключать неэффективные варианты.

Также можно использовать параллельные вычисления для улучшения времени выполнения. Например, задачу можно разделить на независимые подзадачи и выполнять их параллельно на разных ядрах процессора или на разных компьютерах. Это позволит существенно ускорить выполнение задачи и получить результат быстрее.

Наконец, можно провести оптимизацию кода, чтобы ускорить его выполнение. Например, можно устранить избыточные операции, оптимизировать работу с памятью или использовать специальные инструкции процессора для ускорения работы с данными. Такие оптимизации могут значительно ускорить выполнение задачи и снизить время, затрачиваемое на ее решение.

Определение сложности алгоритма

В компьютерных науках понятие сложности алгоритма играет важную роль, поскольку позволяет определить, насколько эффективно данный алгоритм выполняет поставленную задачу. Сложность алгоритма зависит от количества операций, которые выполняются в процессе его работы.

Существует два типа сложности алгоритма: временная сложность и пространственная сложность. Временная сложность алгоритма определяет количество времени, требуемое для его выполнения в зависимости от размера входных данных. Пространственная сложность алгоритма показывает, сколько памяти требуется для выполнения алгоритма.

Сложность алгоритма обычно выражается в виде асимптотической нотации, такой как O-нотация. O-нотация позволяет оценить, как быстро растет время выполнения алгоритма при увеличении размера входных данных. Основные классы сложности алгоритмов в O-нотации: O(1) — постоянная сложность, O(n) — линейная сложность, O(log n) — логарифмическая сложность, O(n²) — квадратичная сложность и т.д.

Определение и анализ сложности алгоритмов помогает разработчикам выбрать наиболее подходящий алгоритм для решения задачи с учетом ограничений по времени и памяти. Кроме того, понимание сложности алгоритма позволяет оптимизировать его выполнение и улучшить производительность программы.

Использование эффективных подходов для решения задачи

Задача со спичками – это интересная головоломка, которая требует от нас логического мышления и творческого подхода. Для решения этой задачи можно использовать несколько эффективных подходов, которые помогут нам найти правильное решение.

Во-первых, стоит начать с анализа предоставленной головоломки. Необходимо внимательно изучить условия задачи и понять, какие ограничения наложены на нас. Затем следует выделить ключевые элементы задачи и обозначить их. Например, спички могут быть обозначены буквами или цифрами, а конечная цель – достижением определенной системы или узора.

Во-вторых, для решения задачи со спичками можно использовать метод проб и ошибок. Не стоит бояться делать ошибки и пробовать разные варианты. При этом стоит записывать каждый шаг и его результаты, чтобы затем анализировать их и искать общие закономерности или шаблоны.

В-третьих, можно использовать алгоритмический подход к решению задачи со спичками. Необходимо осознать, какие действия при выполнении этого алгоритма приведут нас к решению. Например, для создания определенной системы или узора можно использовать комбинации поворотов и перемещений спичек.

В-четвертых, стоит обратиться к опыту и знаниям других людей, которые уже решали данную головоломку. Иногда просто обсуждение задачи с другими людьми может привести к неожиданным и интересным идеям и решениям.

В заключение, для решения задачи со спичками необходимо использовать эффективные подходы, которые помогут нам анализировать условия задачи, использовать метод проб и ошибок, применять алгоритмический подход и обращаться к опыту других людей. Не бойтесь экспериментировать и искать нестандартные решения – это поможет вам развить свою логику и творческое мышление.

Снижение количества необходимых операций

Чтобы снизить количество необходимых операций при решении задачи со спичками, необходимо применять стратегии, которые позволят уменьшить количество ходов или ограничить количество доступных вариантов.

Одна из таких стратегий — использование минимального количества спичек для каждого хода. Если в задаче есть ограничение на количество доступных спичек, то следует выбирать такие ходы, которые требуют использование наименьшего числа спичек.

Еще одна стратегия — использование правил и шаблонов для упрощения задачи. Некоторые задачи со спичками могут быть решены с помощью простого алгоритма, который основан на выявлении определенных шаблонов и применении соответствующих правил.

Например, если задача состоит в создании определенного числа квадратов или треугольников со спичек, можно сократить количество операций, используя шаблоны для построения этих геометрических фигур.

Также следует обращать внимание на возможность использования симметрии или перестановки элементов. Некоторые задачи могут иметь несколько равноценных решений, которые отличаются только расположением или окончательным состоянием спичек.