Как соединить 4 прямыми линиями 9 точек: подробное руководство

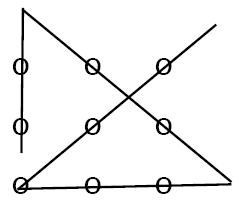
Сочетание точек и линий может создавать удивительные геометрические фигуры. Если у вас есть 9 точек на плоскости, вы можете соединить их 4 прямыми линиями таким образом, чтобы все точки находились на линиях.

Сначала выберите 4 точки, которые будут использоваться как концы прямых линий. Эти точки могут быть любыми из 9 доступных. Затем нарисуйте прямую, проходящую через первую пару выбранных точек. Сделайте то же самое для оставшихся двух пар.

Остальные 5 точек можно соединить с этими 4 прямыми линиями следующим образом: выберите одну из линий и одну из оставшихся точек. Нарисуйте прямую, проходящую через выбранную точку и пересекающуюся с выбранной линией. Повторите этот процесс еще 4 раза для оставшихся точек.

Получившийся результат — 4 прямые линии, которые проходят через все 9 точек. Это геометрическая задача, требующая некоторого воображения и логического мышления. С помощью руководства вы можете легко выполнить эту задачу и изучить фундаментальные принципы геометрии.

Как решить задачу и соединить 4 прямыми линиями 9 точек?

Чтобы решить задачу и соединить 4 прямыми линиями 9 точек, необходимо следовать определенному порядку действий. Первым шагом нужно визуализировать положение точек и отметить их на бумаге или в графическом редакторе.

Затем, чтобы соединить точки прямыми линиями, нужно определить группы точек, которые могут быть соединены одной линией. Для этого можно использовать методика поиска «секвенций» или «циклов». Например, можно начать с соединения трех точек и построения треугольника, а затем составить цепочку, добавив четвертую точку и еще одну прямую.

Важно отметить, что для того чтобы решить задачу, необходимо рассмотреть все возможные комбинации соединения точек. Иногда для решения задачи потребуется использовать дополнительные конструкции или приемы, например, построение перпендикуляров или отсечение линии.

Для удобства, можно сначала построить таблицу, в которой отметить начальные и конечные точки каждой линии. Также, следует использовать эмпирическое мышление и творческий подход при решении задачи, ведь существует несколько вариантов выбора порядка соединения точек.

Начало решения задачи

Для того чтобы соединить 4 прямыми линиями 9 точек, необходимо применить определенную стратегию. В данной задаче, на первый взгляд, внешний вид ее условия может сбить с толку, и покажется, что требуется нарисовать линии через все точки. Однако, это не так.

Чтобы начать решение задачи, необходимо понять, что мы можем соединять точки не только по прямым линиям, но и дугами. Это даёт нам больше свободы и возможностей для поиска решения. В итоге, нам потребуется нарисовать всего 4 линии, проходящие через 9 точек.

Применим метод последовательного подхода, чтобы решить данную задачу. Заметим, что в условии 9 точек разбиты на 3 группы по 3 точки. Будем находить решение для каждой группы по отдельности, а потом объединим полученные решения.

Отметим каждую группу точек числами от 1 до 3, чтобы было легче ориентироваться в дальнейшем. Рассмотрим первую группу точек. Мы можем соединить все её точки одной линией, получив уже 3 соединенные точки. Теперь у нас осталось 6 точек.

Первоначальное понимание задачи

Задача заключается в соединении 9 точек 4 прямыми линиями в такой последовательности, чтобы каждая из линий проходила через все 9 точек и не имела пересечений с другими линиями. Данная задача является головоломкой, требующей логического мышления и креативности для нахождения правильного решения.

Визуализируя задачу, мы можем представить 9 точек, расположенных в виде квадрата, с каждой точкой на углу и в середине каждой из 4 сторон. Чтобы выполнить задачу, нам необходимо провести четыре линии, каждая из которых будет соединять все 9 точек без пересечений.

Первая интуиция может подсказать, что каждая из линий должна проходить через 3 точки. Однако, если мы попытаемся провести 4 линии, каждая из которых содержит по 3 точки, мы столкнемся с проблемой пересечения линий. Поэтому необходимо искать другие варианты.

Ключевой момент в решении задачи заключается в понимании возможного количества точек, через которые может проходить каждая из линий. Для выполнения условий задачи каждая линия должна проходить через не менее двух точек и не более четырех точек.

С учетом этих ограничений, нашей задачей является нахождение последовательности линий и точек, чтобы каждая линия покрывала нужное количество точек и не пересекалась с другими линиями. Для этого можно использовать логическое мышление, искусство рассуждения и пробовать разные варианты соединения точек.

Изучение возможных подходов к решению

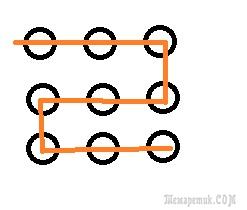
Для решения задачи соединения 4 прямыми линиями 9 точек, необходимо провести анализ возможных подходов и методов решения. Одним из первых методов, который можно использовать, является метод перебора всех возможных комбинаций. Этот метод требует проверки каждой комбинации прямых линий, чтобы убедиться, что они проходят через все 9 точек.

Еще одним методом является метод упорядочивания точек на плоскости, чтобы найти определенные закономерности и упростить задачу соединения линиями. При этом методе можно применить принципы геометрии и использовать графические методы для визуального анализа задачи.

Также можно попробовать использовать алгоритмы соединения точек, которые основаны на определенных математических моделях и правилах. Например, можно применить алгоритм поиска минимального остовного дерева или алгоритм Эйлера для поиска эйлерова цикла в графе.

Необходимо также учитывать, что для решения задачи могут быть использованы как классические методы, так и нетрадиционные и творческие подходы. Возможно, некоторые комбинации линий могут быть рассмотрены в контексте игры «Соедини точки», где можно использовать различные стратегии и логическое мышление для соединения всех точек.

• Метод перебора всех возможных комбинаций
• Метод упорядочивания точек на плоскости
• Алгоритмы соединения точек
• Классические и нетрадиционные методы решения

Подготовка к решению

Перед тем, как приступить к решению задачи о соединении 4 прямыми линиями 9 точек, необходимо подготовиться. Во-первых, рекомендуется ознакомиться с условием задачи и понять, что от вас требуется.

Для начала, можно визуализировать задачу, нарисовав сетку из 9 точек. Это поможет лучше представить себе, как можно соединять эти точки. Также полезно обозначить каждую точку латинской буквой, чтобы легче ориентироваться при решении задачи.

Изучите примеры решений этой задачи, которые можно найти в интернете или в учебниках. Попробуйте самостоятельно нарисовать эти решения на бумаге или в каком-либо графическом редакторе. Это поможет вам лучше понять логику решения и найти свои собственные способы соединения точек.

Кроме того, решение данной задачи часто связано с использованием геометрических принципов и правил. Поэтому, полезно вспомнить основные геометрические термины и свойства, такие как прямая, отрезок, перпендикуляр, параллельность и т.д. Это поможет вам лучше ориентироваться в задаче и применять соответствующие правила при решении задачи.

Необходимые материалы и инструменты

Для выполнения этой задачи вам понадобятся следующие материалы и инструменты:

• Лист бумаги: выберите лист бумаги нужного размера для рисования.
• Карандаши или ручки: возьмите карандаши или ручки разных цветов, чтобы иметь возможность выделить разные элементы в вашем рисунке.
• Линейка: используйте линейку для создания прямых линий и измерения расстояний.
• Клей или скотч: понадобится для скрепления частей вашего рисунка и удержания их вместе.

На странице появится графическое руководство, которое поможет вам определить, как соединять точки прямыми линиями, поэтому необходимо готовить прекрасный материал для рисования. Будьте внимательны и аккуратны при создании своего рисунка.

Разметка и подготовка точек

Перед тем, как приступить к соединению 4 прямыми линиями 9 точек, необходимо разметить и подготовить данные точки.

Прежде всего, важно учитывать, что для соединения всех точек нужно иметь доступ к прямым линиям, которые могут пересекаться друг с другом в различных комбинациях. Поэтому, когда вы размечаете точки, убедитесь, что они расположены таким образом, чтобы в будущем было возможно провести линии согласно условию.

Одним из вариантов разметки точек может быть использование выборочных и последовательно расположенных точек в виде прямоугольника или квадрата. Например, можно разместить точки в виде таблицы или сетки из трех строк и трех столбцов, где каждая ячейка таблицы представляет одну из 9 точек.

Следующим шагом является подготовка точек для соединения. Необходимо убедиться, что каждая точка явно выделена и обозначена. Можно использовать различные способы для этого: написать номера точек рядом с ними, использовать разные цвета для каждой точки или применить другие методы визуальной идентификации. Также полезно будет создать список точек с их описанием или координатами, чтобы было удобно ориентироваться в процессе соединения.

Важно помнить, что точки должны быть четко видны и различимы, чтобы избежать путаницы и ошибок при проведении линий. Когда точки готовы и отмечены, можно приступать к следующему шагу — соединению точек прямыми линиями.

Решение задачи

Чтобы соединить 4 прямыми линиями 9 точек, нам потребуется применить определенную последовательность шагов.

1. Нарисуем на бумаге 9 точек в виде трех горизонтальных линий, расположенных одна под другой. Всего у нас должно получиться три горизонтальных ряда по три точки в каждом.
2. Возьмем карандаш и протянем прямую линию, соединяющую первую точку в первом ряду с первой точкой во втором ряду.
3. На этой же линии, продолжим проводить прямую линию, соединяющую вторую точку во втором ряду с первой точкой в третьем ряду.
4. Проведем третью прямую линию, соединяющую третью точку в первом ряду с третьей точкой во втором ряду.
5. На этой же линии, продолжим проводить прямую линию, соединяющую вторую точку во втором ряду с третьей точкой в третьем ряду.
6. Проведем четвертую прямую линию, соединяющую третью точку во втором ряду с третьей точкой в третьем ряду.

Итак, проведя эти четыре линии, мы соединим все 9 точек, образуя замкнутую геометрическую фигуру.

Первая линия и первая группа точек

Для начала нужно выбрать одну из девяти точек и соединить ее с остальными в первую линию. В данной задаче можно выбрать любую точку в качестве начальной, поэтому выберем первую точку из группы. После выбора начальной точки, нужно провести прямую линию, которая проходит через все остальные точки группы.

Для удобства работы с точками, можно использовать координатную плоскость. На вертикальной оси отмечаются номера точек (сверху вниз), на горизонтальной оси — номера линий (слева направо). В данном случае у нас 9 точек и 4 линии, поэтому все точки помещаются в таблицу 3×3.

Первая линия можно провести, выбирая точки в следующем порядке: первая точка (1,1), вторая точка (2,2), третья точка (3,3) и четвертая точка (1,2).

Теперь у нас есть первая линия, которая проходит через первую группу точек. Для продолжения задачи, нужно перейти к следующей линии и следующей группе точек.

• Первая линия: точка (1,1) — точка (2,2) — точка (3,3) — точка (1,2)

Вторая линия и вторая группа точек

После получения первой линии с помощью прямого соединения трех точек, необходимо перейти к формированию второй линии. Для этого понадобится использовать другую группу из оставшихся точек.

Выберите из оставшихся шести точек новую группу трех точек, которые не соединены между собой и не лежат на одной прямой с уже построенными линиями. При этом можно воспользоваться принципом минимального пересечения линий, чтобы обеспечить наиболее четкое и наглядное соединение.

Визуализируйте вторую группу точек и определите порядок их соединения, чтобы получить вторую линию. После этого прямо соедините первую точку второй группы с одной из крайних точек уже построенной линии.

Продолжите прямое соединение двух оставшихся точек второй группы с другими крайними точками первой линии. Таким образом, получите вторую линию, соединив все точки второй группы с уже построенными линиями.

Третья и четвертая линии и оставшиеся точки

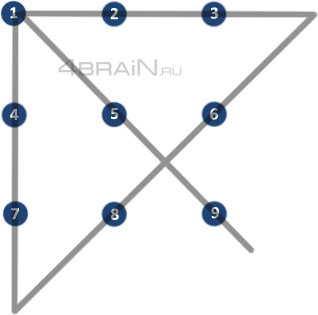
После проведения первых двух линий, остается 4 неразбитых точки. Наша цель — соединить их еще двумя прямыми линиями. Для этого нам потребуется немного фантазии и внимательности.

Для начала, соединим две точки от конца первой линии и от начала второй линии. Возможны два варианта: либо соединяем нижнюю точку первой линии с верхней точкой второй линии, либо наоборот. Проведенная линия будет касаться внутренних точек первой и второй линии.

Затем мы проводим вторую линию, которая соединяет оставшиеся две точки. По сути, это означает, что наша четвертая линия — это либо продолжение верхней части первой линии, либо продолжение нижней части второй линии. Таким образом, все 9 точек соединены и мы успешно завершаем задачу.