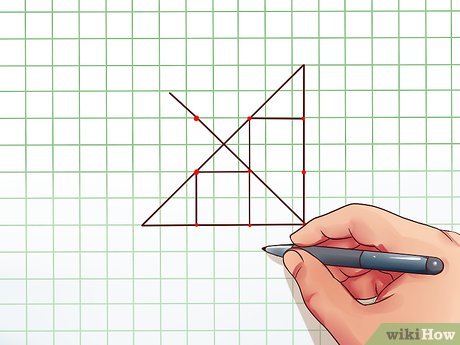
В математике часто возникают интересные задачи, требующие логического мышления и творческого подхода. Одной из таких задач является соединение 9 точек 4 прямыми линиями без отрыва карандаша от бумаги. На первый взгляд может показаться, что это невозможно, однако, существуют простые шаги и хитрости, позволяющие успешно решить эту задачу.
Первым шагом в решении данной задачи является осознание того, что линии могут проходить не только по вертикали и горизонтали, но и по диагонали. Это открывает новые возможности в поиске решения. Ключевым моментом является нахождение точки, которая будет служить «началом» для всех четырех линий.
Одна из хитростей состоит в том, что начальная точка должна находиться за пределами внутреннего квадрата, образованного 9 точками.
Далее, вторым шагом является построение линий, которые будут проходить через каждую из оставшихся 8 точек. При этом важно следить за тем, чтобы линии не пересекались и не подрывали решение. На первый взгляд может показаться сложно, но с помощью рассмотрения различных комбинаций линий можно найти правильное решение.
Таким образом, соединение 9 точек 4 прямыми линиями является задачей, которую можно успешно решить при помощи логического мышления и применения хитростей. Важно помнить, что решение данной задачи не единственно, и существует несколько возможных вариантов. Главное — быть настойчивым и творческим в поиске решения.
Подготовка к заданию
Перед тем, как приступить к решению задания по соединению 9 точек с помощью 4 прямых линиями, необходимо прежде всего понять само задание. Возможно, на первый взгляд оно может показаться достаточно простым, однако требует определенного мыслительного подхода и логики.
Вначале важно визуализировать задание и представить себе 9 точек, расположенных на плоскости. Возможно, поможет нарисовать их на бумаге или использовать воображение для создания ментальной картины. Это позволит лучше ориентироваться в пространстве и понимать, как могут быть соединены эти точки.
Далее следует обратить внимание на ограничивающие условия задания. В данном случае имеется в виду то, что нужно использовать всего 4 прямые линии для соединения всех 9 точек. Это означает, что необходимо продумать наилучший способ соединения, чтобы не нарушить данное условие и обеспечить наилучший результат.
Также следует учесть, что линии могут проходить только через точки, а не вне их. Это ограничение нужно учесть при поиске наилучшего варианта решения задания.
Выбор точек
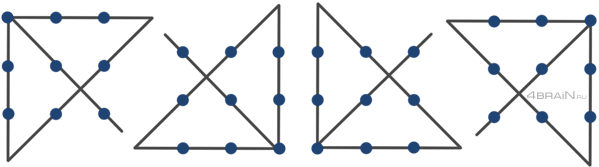
Для соединения 9 точек 4 прямыми линиями необходимо выбрать точки таким образом, чтобы все линии были уникальными и проходили через разные точки. При выборе точек стоит учитывать следующие аспекты:
- Разнообразие расположения: Чтобы создать интересный и красивый рисунок, стоит выбирать точки с разным расположением на плоскости. Разные уровни высоты и разброс точек по горизонтали и вертикали могут сделать рисунок более динамичным и привлекательным.
- Соединение отдаленных точек: Чтобы использовать все 4 прямые линии, стоит выбирать точки, которые находятся геометрически удаленными друг от друга. Это позволит оптимально распределить линии и создать более сложный образец.
- Симметричное расположение: Симметрия может быть интересным элементом рисунка. Попробуйте выбрать точки так, чтобы линии были симметричными относительно осей или других элементов рисунка.
- Связь с окружающим пространством: Рассмотрите возможность связать рисунок с окружающим пространством или другими элементами дизайна. Например, создайте линии, которые продолжаются за пределами изображения или соединяются с другими объектами.
Выбор точек является важным этапом в создании рисунка, так как определит его структуру и эффект. Используйте свою креативность и экспериментируйте с разными вариантами расположения точек, чтобы получить уникальный и интересный результат.
Расположение точек
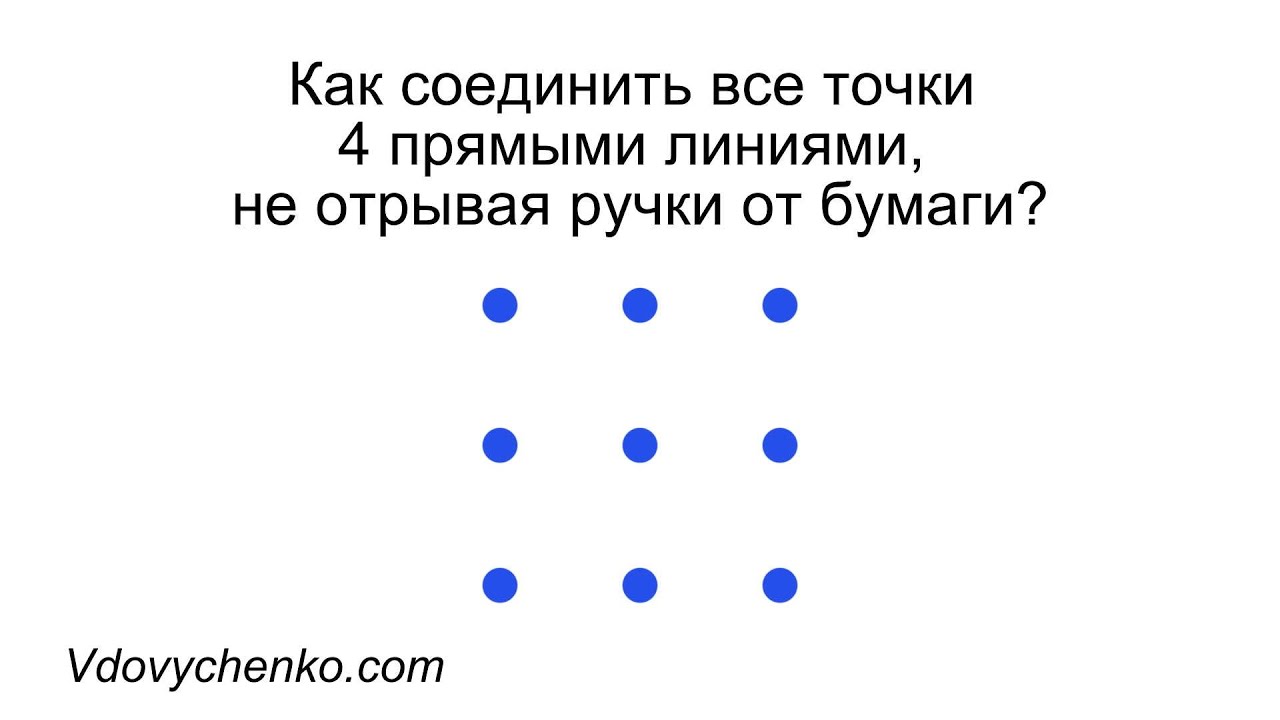
Чтобы решить задачу о соединении 9 точек 4 прямыми линиями, важно понимать их расположение. Самая простая и понятная схема расположения точек — это 3 строки по 3 точки в каждой. При такой схеме мы можем визуально представить точки как клетки на игровом поле.
Когда мы рассматриваем такую схему расположения точек, становится понятно, что две точки находятся на одной горизонтали или вертикали, а остальные точки находятся на разных диагоналях. Это значит, что нам придется использовать прямые линии, проходящие не только по горизонтали и вертикали, но и по диагонали.
Чтобы решить задачу, можно воспользоваться несколькими стратегиями. Во-первых, можно попробовать провести прямые линии, соединяющие точки, и обратиться к графическому изображению, чтобы найти паттерн или систему, которую необходимо использовать. Во-вторых, можно проделать несколько попыток и проверить, что получается. В-четвертых, можно использовать математическую логику, чтобы проследить линии и выявить определенные закономерности.
Расположение точек может быть использовано для создания различных комбинаций из линий. Необходимо экспериментировать и искать варианты, которые будут соответствовать условию задачи. В зависимости от точек и их расположения, мы можем прийти к логическому решению. Не стесняйтесь использовать карандаш и бумагу для рисования и экспериментов. Постепенно, вы сможете улучшить свои навыки и найти оптимальное решение.
Шаги выполнения

Для выполнения данной задачи необходимо следовать нескольким простым шагам:
- Нарисуйте на листе бумаги 9 точек, расположенных в виде квадрата 3х3.
- Соедините первую и вторую точку прямой линией. Проделайте ту же операцию для третьей и четвертой точки, а также для пятой и шестой точки.
- Соедините вторую и третью точку прямой линией. Затем соедините четвертую и пятую точку, а также шестую и седьмую точку.
- Проделайте ту же операцию для пятой и шестой точки, а также для седьмой и восьмой точки.
- Соедините шестую и девятую точку прямой линией.
После выполнения всех шагов у вас получится 9 точек, соединенных четырьмя прямыми линиями.
Первая линия
Для того чтобы нарисовать первую линию, вам необходимо выбрать три точки из девяти имеющихся на поле. Важно выбрать такие точки, которые находятся на одной прямой линии. Поверьте, это не так просто, как кажется. Попробуйте разные комбинации и ищите тройки точек, которые образуют прямую.
Запомните, что допускается использовать как горизонтальные, так и вертикальные линии. Поэтому не ограничивайте себя только горизонтальными или вертикальными точками. Если вы найдете три точки, которые образуют прямую, соедините их линией. Получившаяся прямая будет вашей первой линией.
Обратите внимание на последовательность выбора точек. Она может повлиять на возможность построения остальных линий. Поэтому не забывайте анализировать свои действия и искать оптимальное расположение точек для построения следующей линии.
Вторая линия
Чтобы создать вторую линию, необходимо ориентироваться на точки, которые остались после проведения первой линии. Представьте, что начало второй линии соединяет угол, с образовавшимся треугольником. Ваша задача — провести линию из этого угла через одну из оставшихся точек.
Для построения второй линии у вас есть несколько вариантов: вы можете выбрать точку, находящуюся на противоположной стороне от начала первой линии, или точку, которая находится сбоку от начала первой линии. В любом случае, подумайте о направлении линии и убедитесь, что она будет проходить через нужную точку.
Помните, что вторая линия должна быть прямой и проходить через одну из оставшихся точек. Используйте свою фантазию и экспериментируйте с различными вариантами, чтобы найти самый оптимальный способ соединения точек. Возможно, вам потребуется несколько попыток, чтобы найти правильный маршрут, но это лишь часть процесса.
Третья линия
При соединении 9 точек 4 прямыми линиями третья линия играет ключевую роль в формировании решения. Она должна пересекать две предыдущие линии и проходить через оставшиеся точки.
Чтобы найти правильное направление третьей линии, важно отметить, что она должна пройти через одну из угловых точек. Это обеспечивает оптимальное использование пространства и позволяет соединить все точки.
Выбрав стартовую угловую точку, следует проложить линию, которая пересечет первую и вторую линии в одной из центральных точек. Затем, продолжая линию дальше, нужно обратить внимание на пересечение с третьей линией. Чтобы создать пересечение, можно использовать угловую точку, либо вводить дополнительную точку.
Третья линия активно взаимодействует с остальными линиями, поэтому важно учитывать их направление и взаимное расположение. Используя эффектные ходы и стратегические действия, можно достичь интересных и неожиданных решений проблемы соединения 9 точек 4 прямыми линиями.
Хитрости и советы
1. Пробуйте разные варианты: Если вы не можете соединить все девять точек четырьмя прямыми линиями сразу, не паникуйте. Попробуйте использовать разные комбинации линий для соединения точек. Иногда неочевидные варианты могут оказаться правильными.
2. Думайте за пределами прямых линий: Возможно, не все соединения точек должны быть прямыми линиями. Рассмотрите возможность использования дуг или кривых для соединения точек. Это может открыть новые варианты и упростить задачу.
3. Работайте с шаблонами: Некоторые шаблоны могут быть полезны для решение задачи. Используйте таблицу 3×3, чтобы наглядно представить все возможные соединения точек и прямых линий. Это поможет вам систематизировать свои идеи и найти правильное сочетание.
4. Не зацикливайтесь на одном пути: Если вы не можете найти решение с помощью одной конкретной стратегии, попробуйте изменить свой подход. Поменяйте точки, с которых вы начинаете или прекратите использовать определенные линии. Иногда даже небольшие изменения могут привести к открытию нового решения.
5. Общайтесь с другими: Если вы не можете найти решение самостоятельно, попробуйте обсудить проблему с другими людьми. Они могут предложить новые идеи и подходы, которые вы не рассмотрели. Коллективное мышление часто приводит к новым и инновационным решениям.
6. Используйте эмпирический метод: Если все остальные попытки не увенчались успехом, попробуйте просто нарисовать линии, не задумываясь о правильном решении. Иногда простая интуиция или случайно нарисованные линии могут привести к верному ответу. Не бойтесь экспериментировать!
Использование диагональных линий
Для того чтобы соединить 9 точек 4 прямыми линиями, можно использовать диагональные линии. Диагональные линии — это линии, которые соединяют точки не по прямой, а по диагонали.
Чтобы использовать диагональные линии, нужно провести линии, которые идут под углом, а не прямо. Например, можно начать соединять точки по вертикали или горизонтали, а затем провести диагональные линии, чтобы закрыть оставшиеся отрезки между точками.
Важно помнить, что диагональные линии должны быть прямыми и проходить через точки, которые нужно соединить. Линия должна соединять точки без пересечения с другими линиями.
Диагональные линии могут быть использованы в игре «соедини точки» или при решении головоломок на математическую логику. Использование диагональных линий позволяет более эффективно соединять все точки и создает интересный и красивый образец.
Пересечение линий

Пересечение линий — важный элемент в решении задачи о соединении 9 точек с помощью 4 прямых линий. Для успешного выполнения задачи необходимо верно определить точки пересечения, чтобы соединить все точки и не нарушить условия задачи.
Чтобы определить точки пересечения, необходимо провести уже известные линии и найти их пересечения с другими линиями. Затем, используя полученные точки пересечения, можно провести новые линии, включающие эти точки. Таким образом, постепенно будут соединены все 9 точек, получив нужную структуру.
Для более наглядного представления, можно использовать таблицу, в которой будут указаны уже проведенные линии и их точки пересечения. Это поможет лучше видеть, какие точки еще необходимо соединить и какие линии уже проведены.
Необходимо помнить, что в процессе соединения линий может возникнуть несколько вариантов точек пересечения. В этом случае можно использовать подход «проб и ошибок», пытаясь провести линии и проверяя, правильно ли они пересекаются.
Пересечение линий является одним из ключевых моментов в решении задачи о соединении 9 точек с помощью 4 прямых линий. Правильно определенные точки пересечения позволят успешно выполнить задачу и получить желаемый результат. А использование таблицы и подхода «проб и ошибок» помогут упростить процесс и улучшить результат.








