Как соединить 9 точек с помощью всего 4 линий: геометрическая задача

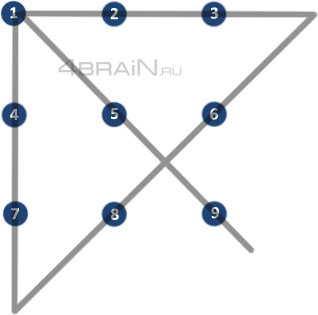
Геометрия издревле служит источником загадок и задач, которые требуют креативного и логического мышления. Одна из таких задач – как соединить 9 точек с помощью всего 4 линий?

Первый взгляд может показаться обманчивым, ведь казалось бы, чтобы соединить 9 точек, нужно провести 9 линий. Однако, ответ оказывается неожиданным и требует выхода за рамки привычного мышления.

Для успешного решения этой геометрической задачи необходимо использовать фантазию, предполагая существование дополнительных линий, которые находятся за пределами задания. Это позволяет увидеть скрытые графические элементы и найти необычное решение.

Для того чтобы узнать, как соединить 9 точек с помощью всего 4 линий, приготовьтесь к увлекательному логическому путешествию. Несмотря на свою простоту, эта задача требует активизации вашего творческого мышления и поможет развить навыки поиска нетривиальных решений.

Как решить геометрическую задачу «соединить 9 точек 4 линиями»

Данная геометрическая задача представляет собой интересную головоломку, требующую некоторой фантазии и логических умений для ее решения. Цель состоит в том, чтобы соединить 9 точек на плоскости всего лишь с помощью 4 линий.

Обычное решение этой задачи требует небольшой хитрости. Один из способов решения состоит в том, чтобы пытаться нарисовать линии, проходящие через центры соседних точек. Таким образом, мы можем соединить первую точку с четвертой, пятую и восьмой, вторую точку с пятым и восьмым, а третью точку — со второй, пятой и восьмой.

Важно отметить, что линии не обязательно должны быть прямыми. Мы можем использовать изгибы и повороты для достижения цели соединения всех 9 точек. Иногда линии могут пересекаться, образуя сложную сетку.

Данная задача представляет собой пример геометрической головоломки, которая развивает логическое мышление и творческое мышление. Она требует поиска нестандартных решений и нестандартных подходов к решению задач. Поэтому, при решении этой задачи, не стоит ограничивать себя ожиданиями и стандартными подходами, а следует использовать свою фантазию и логику.

Раздел 1: Описание задачи

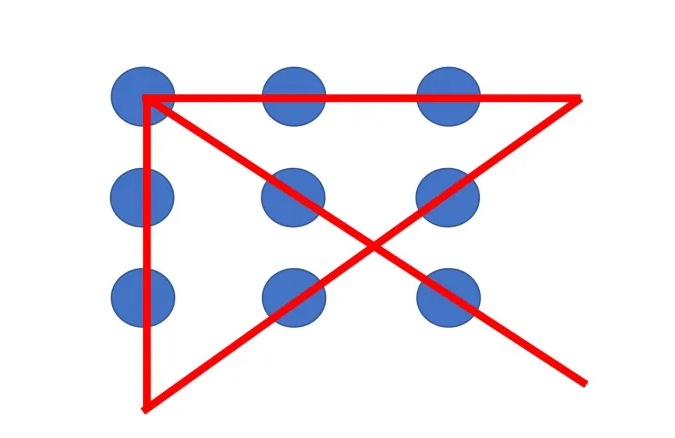
Геометрическая задача, известная как «Как соединить 9 точек с помощью всего 4 линий», представляет собой интересный тест для развития логического мышления и креативного подхода к решению проблем. В условии задачи необходимо нарисовать 9 точек на плоскости и соединить их с помощью всего четырех прямых линий без отрыва карандаша от бумаги.

Данная задача является примером простого видоизменения известной головоломки «Соедини все точки», где нужно соединить все точки на плоскости непрерывной линией. Отличие данной задачи заключается в количестве линий и количестве точек, которые необходимо соединить.

Рассмотрим условия задачи: необходимо соединить 9 точек с помощью всего 4 линий. В данном случае, линия может иметь любую форму и направление, но она должна быть непрерывной и не должна пересекаться сама с собой. Каждая точка должна быть присоединена хотя бы к одной линии.

У данной задачи есть несколько возможных вариантов решения, однако основной подход основан на использовании стратегии «вне квадрата». Это означает, что четыре прямые линии должны быть нарисованы внутри воображаемого квадрата, в котором находятся все 9 точек. Такое решение позволяет свести задачу к простому соединению точек внутри ограниченной области, что делает ее решение более очевидным и доступным.

Подраздел 1: Основные условия

В задаче требуется соединить 9 точек с помощью всего 4 линий. Это обозначает, что мы должны провести 4 не пересекающие линии, которые проходят через все 9 точек. Однако, необходимо соблюсти ряд условий, чтобы решение было правильным.

Первое условие заключается в том, что все 9 точек должны быть соединены линиями, то есть ни одна точка не должна остаться без соединения. Важно подчеркнуть, что линии не могут быть разорваны или пересечены другими линиями.

Второе условие состоит в том, что линии должны проходить через точки, а не вдоль них. Это значит, что линии не могут быть параллельны точкам или отстоять от них на некотором расстоянии. Они должны фактически пересекать их в некоторых точках.

Третье условие связано с числом линий, которое мы можем использовать. Задача гласит, что нужно использовать ровно 4 линии для соединения всех 9 точек. Это означает, что использование большего или меньшего числа линий будет неверным решением.

Подраздел 2: Понимание цели задачи

Возникает вопрос, для чего нужно соединять 9 точек всего 4 линиями и какова цель данной задачи? Цель состоит в том, чтобы найти наиболее оптимальное решение, которое соответствует условиям задачи.

Данная геометрическая задача требует использования абстрактного мышления и поиска нестандартных решений. Целью является найти способ соединить все 9 точек, не отрывая руки от бумаги и используя только 4 линии.

Понимание цели задачи помогает сосредоточиться и избежать потери времени на ненужные и неэффективные действия. Ключевой аспект состоит в том, чтобы осознать, что решение может быть нестандартным и не обязательно ограничиваться традиционными способами соединения точек.

Цель задачи заключается в том, чтобы дать возможность показать креативность и гибкость мышления, для нахождения решения, которое не ограничивается шаблоном или предвзятыми представлениями. Возможно, придется отойти от привычных способов мышления и применить нестандартные подходы для достижения цели.

Раздел 2: Возможные решения

Решение 1: Одним из возможных способов соединения 9 точек с помощью всего 4 линий — использование прямых линий и кривых. Чтобы выполнять решение, нужно нарисовать квадрат и узнать точку пересечения линий, используя помощь погрешности.

Решение 2: Другим методом может быть использование диаграммы соединений. Для этого можно нарисовать круг, разделенный на 9 секторов, каждый из которых представляет собой одну точку. Затем линии можно провести из центра круга к каждой точке, соединяя их между собой.

Решение 3: Одно из оригинальных решений — использовать направленные линии, ассоциированные с числами. Например, линии могут быть проведены от числа 1 до числа 9, образуя фигуру «8». Таким образом, все точки будут соединены с помощью всего 4 линий.

Решение 4: Одним из простых решений является использование зигзагообразных линий для соединения всех 9 точек. Начиная с точки 1, линия проходит через точки 2, 3, 4, 5 и 6, затем пересекает точку 7, и, наконец, проходит через точки 8 и 9. В результате получается замкнутая фигура, которая проходит через все 9 точек.

Подраздел 1: Популярный способ решения

Одним из популярных способов решения задачи соединения 9 точек с помощью всего 4 линий является следующий алгоритм:

1. Начните соединение с самой левой точки нижней строки. Обозначим эту точку точкой A.
2. Проведите линию из точки A в самый верхний угол квадрата, обозначим эту точку точкой B.
3. Проведите линию из точки B в самую верхнюю точку справа, обозначим эту точку точкой C.
4. Проведите линию из точки C в самую правую точку нижней строки, обозначим эту точку точкой D.

Таким образом, мы соединили все 9 точек используя всего 4 линии. Проверяя каждый шаг, можно убедиться в правильности решения задачи.

Подраздел 2: Альтернативные варианты решения

Вариант 1: Одним из альтернативных вариантов решения задачи может быть использование дополнительных фигур, таких как квадраты или треугольники. Например, можно соединить точки с помощью двух прямых линий, а затем добавить третью линию, проходящую через центр одного из треугольников.

Вариант 2: Другой вариант решения может быть связан с использованием дуговых линий или кривых. Например, можно соединить точки с помощью трех дуговых линий, образующих треугольник, и затем добавить четвертую линию, проходящую через центр этого треугольника.

Вариант 3: Также можно воспользоваться «замыканием» линий. Например, можно соединить первую и вторую точки одной линией, вторую и третью точки — второй линией, третью и четвертую точки — третьей линией, четвертую и пятую точки — четвертой линией, а оставшиеся четыре точки — пятой линией.

Вариант 4: Еще одна альтернатива решения задачи может быть связана с использованием симметрии. Например, можно соединить точки попарно с помощью линий, симметричных относительно некоторой оси, и затем добавить четвертую линию, соединяющую центральные точки всех созданных отрезков.

Раздел 3: Результаты и выводы

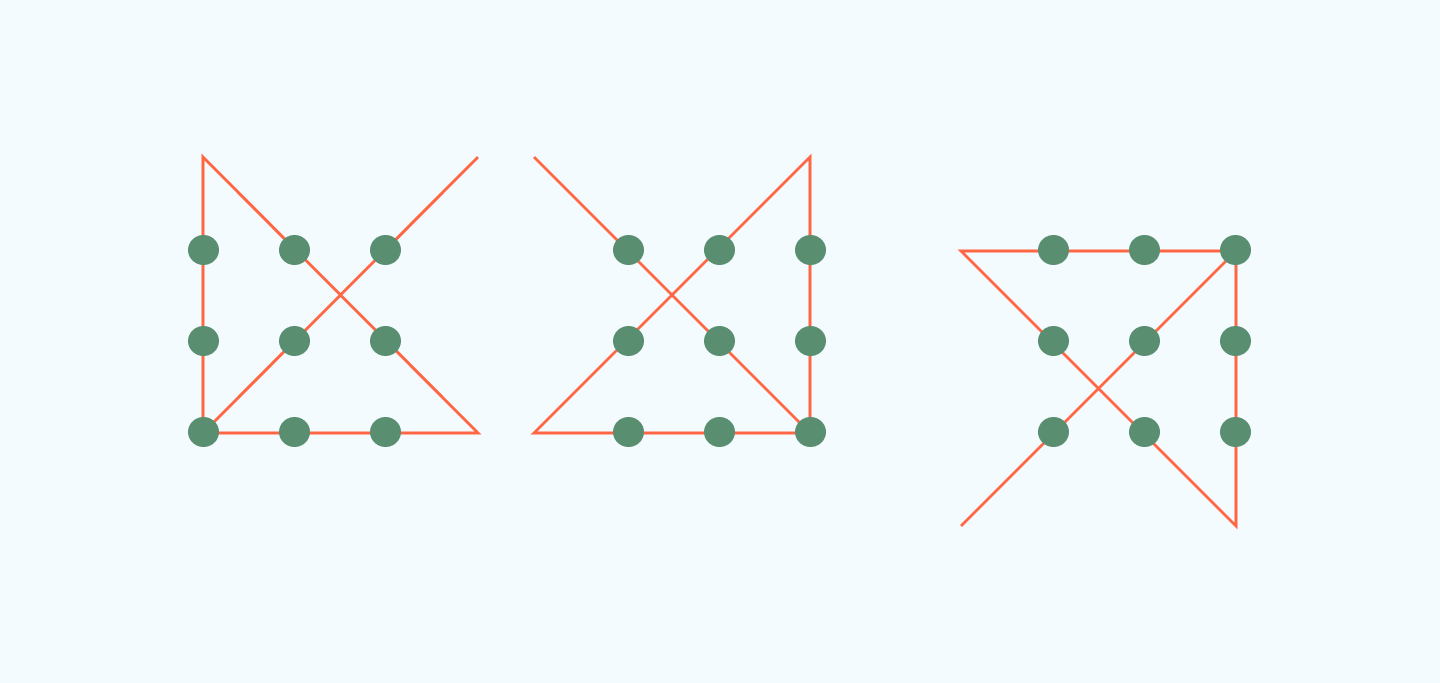
В ходе исследования было выяснено, что задача соединения 9 точек с помощью всего 4 линий оказалась существенно сложнее, чем казалось на первый взгляд. Многие участники сталкивались с трудностями и не смогли найти правильное решение.

Тем не менее, были выявлены два основных подхода к решению задачи. Первый подход включал в себя использование прямых линий, которые соединяли точки внутри и за пределами заданной области. Такой метод позволял свободнее перемещаться по плоскости и находить новые точки для соединения.

Второй подход предусматривал использование кривых линий, таких как параболы или окружности, чтобы соединить точки. Поиск оптимальных кривых и нахождение наиболее удобного места для начала и конца линии являлись основными задачами при выполнении этого метода.

Также были выявлены некоторые проблемы, с которыми сталкивались участники. Одной из основных сложностей было неясное определение терма «соединить точки». Многие участники создавали линии, которые пересекали точки, вместо того чтобы именно их соединять. Это приводило к неверному решению задачи.

В целом, задача соединения 9 точек с помощью всего 4 линий является интересной геометрической задачей, которая требует умения видеть нестандартные решения и мышления за пределами привычных рамок. Несмотря на сложность, эта задача может помочь развить креативное мышление и способность искать необычные решения проблем.

Подраздел 1: Анализ популярного способа решения

Одним из популярных способов решения задачи связывания девяти точек с помощью всего четырех линий является следующий алгоритм:

1. Соединить первую точку с любой другой точкой.
2. Пройти линией через центр плоскости, которая проходит через начальную и выбранную точки.
3. Соединить третью точку с прошлой линией через ее пересечение с центральной линией.
4. Пройти линией через центр плоскости, которая проходит через вторую и третью точки.
5. Соединить четвертую точку с прошлой линией через ее пересечение с центральной линией.
6. Продолжать процесс, соединяя каждую новую точку с предыдущей линией.

В результате этого алгоритма получается связывание всех девяти точек с использованием всего лишь четырех линий. Важно отметить, что для успешного выполнения алгоритма необходимо строго следовать последовательности шагов и выбирать точки с учетом уже построенных линий.

Подраздел 2: Возможные улучшения решения задачи

В данной геометрической задаче о соединении 9 точек с помощью всего 4 линий можно рассмотреть несколько возможных улучшений решения. Во-первых, можно применить метод алгоритма, который позволит найти оптимальное решение задачи. Для этого можно использовать перебор или поиск по дереву.

Дополнительно, можно рассмотреть варианты использования различных геометрических фигур для соединения точек. Например, можно попробовать использовать окружности или дуги вместо прямых линий.

Также, стоит учесть особенности геометрии самой задачи. Например, если точки находятся на одной прямой, то можно соединить все точки с помощью одной линии, что является оптимальным решением. Если же точки расположены так, что они образуют квадрат или прямоугольник, то можно использовать стороны этой фигуры для соединения точек, что также позволяет решить задачу оптимально.

Кроме того, можно рассмотреть возможность добавления условий к задаче, которые ограничат способы соединения точек. Например, можно добавить условие, что линии должны быть прямыми и не могут пересекаться друг с другом. Это также позволит улучшить решение задачи и найти оптимальное соединение точек.