Как соединить девять точек четырьмя линиями: уникальные методы и подсказки

Соединение девяти точек четырьмя линиями является интересной задачей, которая может вызвать затруднения у многих. Однако существуют уникальные методы и подсказки, которые помогут вам решить эту головоломку. В этой статье мы рассмотрим несколько вариантов, которые позволят вам успешно выполнить данное задание.

Первый метод заключается в использовании стратегии «разделения и правления». Для этого вы можете поделить точки на группы и соединить их внутри каждой группы. Затем соедините отдельные группы с помощью линий, чтобы получить искомое соединение. Этот метод требует некоторой дополнительной логики и анализа, но в конечном итоге позволяет достичь желаемого результата.

Еще один метод заключается в использовании геометрических форм. Перед вами стоят девять точек, которые можно разместить в виде квадрата или других геометрических фигур. Используя эти формы, вы можете легко соединить точки четырьмя линиями, следуя заданному порядку. Этот метод может быть особенно полезен для визуального восприятия задачи и нахождения решения.

Наконец, стоит упомянуть об использовании сложных алгоритмов и математических концепций для решения этой задачи. Например, можно применить теорему о связности графа или концепцию гамильтонова пути. Эти методы требуют более продвинутых знаний и навыков, но могут быть использованы для успешного соединения точек четырьмя линиями.

Важно помнить, что решение этой головоломки может не быть единственным. Каждый метод имеет свои преимущества и недостатки, и возможно, вам потребуется пробовать разные способы для достижения желаемого результата. Важно сохранять гибкость и творчески подходить к решению задачи.

Как решить задачу «как соединить девять точек четырьмя линиями: уникальные методы и подсказки»

Задача о соединении девяти точек четырьмя линиями является одной из самых известных головоломок в математике. Возможностей решения этой задачи существует несколько, и каждая из них представляет свой уникальный метод и подход.

Один из способов решения задачи заключается в использовании принципа пересечений. Для этого необходимо провести четыре линии таким образом, чтобы они пересекались и образовывали замкнутую фигуру, проходящую через все девять точек. Этот метод требует внимательного анализа и экспериментирования, чтобы найти оптимальное решение.

Другой метод основан на использовании геометрических форм и симметрии. Можно представить задачу о соединении девяти точек, как квадрат, состоящий из девяти маленьких квадратов. Проведя четыре линии по границам этих маленьких квадратов, мы сможем соединить все девять точек. Этот подход основан на принципе симметрии и позволяет решить задачу эффективно и легко.

Также можно воспользоваться таблицей соединений, которая показывает все возможные способы соединения точек четырьмя линиями. Эта таблица помогает упорядочить и систематизировать возможные варианты решения задачи. При использовании этого метода особое внимание следует уделить анализу и выбору оптимальных соединений.

Раздел 1: Метод «треугольник и квадрат»

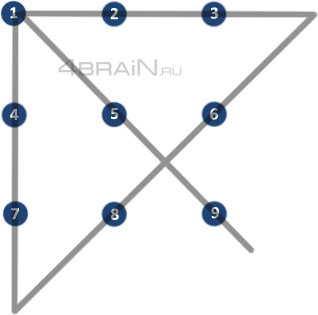
Один из уникальных методов для соединения девяти точек четырьмя линиями – метод «треугольник и квадрат». Этот метод основан на использовании геометрических фигур – треугольника и квадрата – для соединения точек.

Для начала, выберите три точки, которые образуют треугольник. Соедините эти точки линиями, образуя треугольник. Затем, выберите одну из оставшихся точек и соедините ее с одной из вершин треугольника, так чтобы получился прямоугольник.

Повторите этот шаг еще два раза, выбирая оставшиеся точки и соединяя их с вершинами треугольника, пока не будут использованы все девять точек. В итоге, вы получите четыре линии, соединяющие все девять точек.

Метод «треугольник и квадрат» является одним из эффективных способов для соединения девяти точек. Он позволяет задействовать геометрические фигуры, что делает решение задачи более интересным и красочным. Попробуйте использовать этот метод и посмотрите, как он может быть полезен вам при решении данной задачи.

Подраздел 1: Разделим точки на три группы

Процесс соединения девяти точек четырьмя линиями может быть достаточно сложным, но с правильным подходом можно найти решение. Первый шаг в решении этой задачи — разделить все точки на три группы.

Для начала обратим внимание на самую внешнюю группу точек — это точки, которые находятся на периферии. Всего таких точек должно быть четыре. Мы можем обозначить их как A, B, C и D. Затем, из оставшихся пяти точек выберем три на внутренней периметрии. Обозначим их как E, F и G.

Теперь перейдем к внутренней группе точек, которая находится внутри внешнего периметра. Здесь также будет три точки, обозначим их как H, I и J. Последняя группа точек, которую мы обозначим как K, будет состоять из единственной точки находящейся внутри предыдущей группы.

Таким образом, мы разделили все девять точек на три группы: внешнюю, внутреннюю и точку внутри последней группы. Это первый шаг к поиску решения задачи и поможет нам лучше ориентироваться в следующих этапах.

Подраздел 2: Соединим точки в каждой группе

Для успешного соединения девяти точек четырьмя линиями, необходимо правильно составить группы точек. Разбиваем наши девять точек на три группы — по три точки в каждой группе. Теперь начинаем соединять точки внутри каждой группы.

В первой группе соединяем первую точку со второй, вторую с третьей, а затем третью с первой. Получаем треугольник, внутри которого находятся три точки.

Переходим ко второй группе. Тут уже соединяем первую точку с третьей, вторую с первой и третью с второй. Таким образом, получаем второй треугольник, который также содержит три точки.

В третьей группе соединяем первую точку со второй, вторую с третьей и третью с первой. И вот, третий треугольник готов.

Теперь наши группы точек превратились в три треугольника. Осталось только соединить эти треугольники между собой четырьмя линиями. Но об этом мы расскажем в следующем подразделе.

Подраздел 3: Проведем линии между группами

Один из способов соединить девять точек четырьмя линиями — провести линии между группами точек. Для этого необходимо разделить все точки на три группы, каждая из которых будет содержать три точки. Далее можно провести линии между центрами масс каждой группы точек.

Для более наглядной визуализации можно использовать таблицу с тремя строками и тремя столбцами. В каждой ячейке таблицы будут помещены координаты одной точки. Затем с помощью HTML и CSS можно разделить таблицу на три равные группы и провести линии между центрами масс каждой группы.

Такой метод позволяет соединить все девять точек четырьмя линиями и при этом сохранить некую симметрию в расположении линий. Однако для реализации данного подхода необходимо иметь некоторые навыки в разработке веб-страниц и использовании языка разметки HTML.

Раздел 2: Метод «центральная точка и линии»

Метод «центральная точка и линии» является одним из уникальных подходов к соединению девяти точек четырьмя линиями. В этом методе используется особая стратегия, которая основана на определении центральной точки и соединении остальных точек линиями.

Начнем с определения центральной точки. Для этого можно визуально оценить расположение точек и выбрать одну из них, которая кажется наиболее центральной. После определения центральной точки, необходимо провести линии из данной точки ко всем остальным.

Следующий шаг — соединение оставшихся точек линиями. В этом методе можно использовать несколько стратегий. Например, можно провести линии из центральной точки к двум точкам, а затем провести линию между этими двумя соединенными точками. Таким образом, мы используем только три линии для соединения четырех точек.

Для лучшего понимания метода «центральная точка и линии» можно создать эскиз или диаграмму, отображающую расположение точек и соединения между ними. Это поможет наглядно представить последовательность действий и убедиться в правильности применяемой стратегии.

Подраздел 1: Определите центральную точку

Перед тем, как приступить к задаче соединения девяти точек четырьмя линиями, необходимо определить центральную точку. Это важный шаг, который поможет вам лучше ориентироваться в задании и правильно распределить свои линии.

Центральная точка — это точка, которая будет находиться в центре вашего рисунка и служить отправной точкой для соединения остальных девяти точек.

Определить центральную точку можно несколькими способами. Один из них — использование геометрического подхода. Разделите область, в которой находятся девять точек, на четыре равные части с помощью двух вертикальных и двух горизонтальных линий. Точка пересечения этих линий будет вашей центральной точкой.

Другой способ — использование математической формулы для определения среднего значения координат всех девяти точек. Найдите сумму всех координат по оси X и разделите ее на 9. То же самое сделайте с координатами по оси Y. Полученные значения будут координатами вашей центральной точки.

Подраздел 2: Проведите линии из центральной точки до остальных

Для того чтобы соединить девять точек с помощью четырех линий, можно начать с проведения линий из центральной точки до остальных.

Сначала следует определить центральную точку на плоскости, что позволит нам установить начало рисования линий. Затем проведите линии из центральной точки до остальных восьми точек. Это поможет нам создать основу фигуры и упростить дальнейшую работу с линиями.

Когда все линии из центральной точки проведены, можно приступить к соединению остальных точек с помощью оставшихся линий. Важно помнить, что линии должны быть прямыми и не пересекаться между собой.

Проведение линий из центральной точки до остальных является одним из методов, который помогает в решении задачи соединения девяти точек четырьмя линиями. Этот подход обеспечивает логическую и последовательную связь между точками, что в конечном итоге позволяет нам создать искомую фигуру.

Подраздел 3: Соедините оставшиеся точки линиями

Когда остаются несоединенные точки, можно использовать несколько приемов, чтобы провести линии между ними и завершить задачу. Один из способов — использовать дополнительные линии, которые пересекаются с уже нарисованными линиями. Это позволит вам создать новые отрезки и соединить оставшиеся точки.

Еще один метод — использовать кривые линии. Вы можете нарисовать плавные изгибы, чтобы соединить оставшиеся точки. Это создаст более сложную и интересную композицию, отличную от обычных прямых линий.

Если у вас осталась только одна точка, которую нужно соединить с остальными, вы можете использовать метод «спирального рисунка». В этом случае вы начинаете соединение с одной точки, затем нарисовать линию, которая поворачивает вокруг себя и проходит через остальные точки, образуя спиральную форму.

Если у вас есть пересекающиеся линии, вы можете использовать цветные маркеры или карандаши, чтобы выделить эти точки и линии на рисунке. Это поможет вам не пропустить ни одной точки и убедиться, что все они соединены вам нужным образом.

Важно помнить, что соединение точек линиями — это не только логическая задача, но и творческий процесс. Не бойтесь экспериментировать с различными методами и искать свой собственный уникальный способ соединения точек, который подходит именно вам.

Раздел 3: Метод «непрерывные обходы»

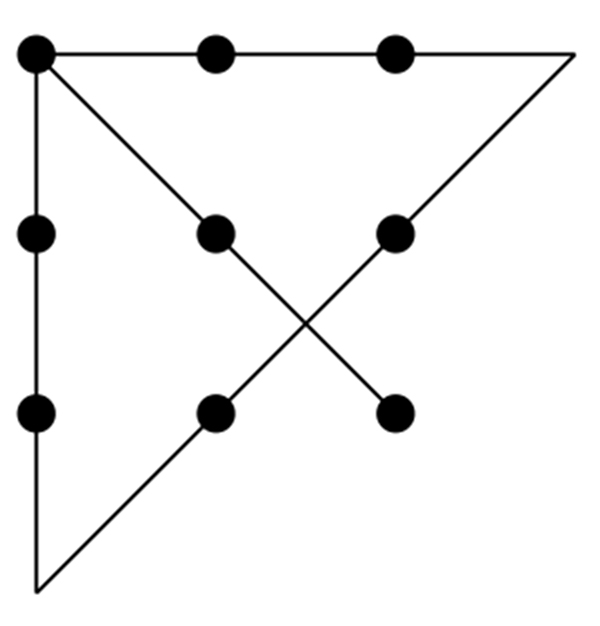
Метод «непрерывные обходы» является одним из эффективных методов решения задачи соединения девяти точек четырьмя линиями. В отличие от других подходов, этот метод допускает движение по всем точкам без перерыва, что позволяет связать все точки за минимальное количество ходов.

Основная идея метода заключается в том, чтобы разбить плоскость на несколько зон и обойти все точки в каждой зоне, а затем связать зоны друг с другом. Это позволяет избежать замкнутых контуров и перекрестков.

Для применения метода «непрерывные обходы» необходимо осуществить следующие шаги:

1. Разделить все точки на несколько групп, пронумеровав их.
2. Соединить каждую группу точек внутри зоны в порядке их нумерации.
3. Связать зоны между собой, соединив последнюю точку одной зоны с первой точкой следующей зоны.

Непрерывные обходы позволяют создать связь между всеми точками исходной задачи с помощью всего лишь четырех линий. Однако, необходимо учитывать, что этот метод требует тщательного планирования и организации точек на плоскости.

Подраздел 1: Начните обход с одной из вершин

Для того чтобы соединить девять точек четырьмя линиями, можно начать обход с одной из вершин. Этот метод основан на принципе поиска пути по графу, где вершины представляют собой точки, а ребра — линии, соединяющие эти точки.

Первым шагом необходимо выбрать одну из вершин в качестве стартовой точки. Затем нужно выбрать следующую точку, которая должна быть соединена с предыдущей линией. Для этого можно использовать различные критерии, например, выбирать точку, которая является ближайшей к предыдущей точке или выбирать точку с наибольшим количеством соседей.

После выбора следующей точки нужно провести линию между текущей и предыдущей точкой. Затем необходимо продолжить процесс выбора следующей точки и проведения линий до тех пор, пока не будут соединены все девять точек.

Важно отметить, что при использовании этого метода может возникнуть ситуация, когда невозможно провести линию между двумя точками без пересечения уже проведенных линий. В таком случае следует отклонить выбор текущей точки и попытаться выбрать другую точку для продолжения обхода.

Подраздел 2: Переходите от вершины к вершине, соединяя их линиями

При решении задачи о соединении девяти точек четырьмя линиями, одним из эффективных методов является переход от вершины к вершине, соединяя их линиями. Это подразделение задачи на более маленькие задачи, что делает ее выполнение более удобным и понятным.

Для начала, выберите одну из вершин и соедините ее с оставшимися восемью вершинами линиями. Затем выберите вторую вершину и соедините ее с оставшимися семью вершинами. Продолжайте этот процесс, пока все вершины не будут соединены линиями.

Важно помнить, что каждая линия должна соединять две разные вершины и не должна пересекать другие линии. Каждая вершина должна быть соединена линией хотя бы с одной другой вершиной.

Данный метод можно представить в виде таблицы, где в строках указаны вершины, а в столбцах — линии. В каждой ячейке таблицы указывается, с какой вершиной соединена данная линия. После заполнения таблицы, можно визуализировать результат, соединяя указанные вершины линиями и получая искомый путь, проходящий через все вершины.

Подраздел 3: Завершите обход в исходной вершине

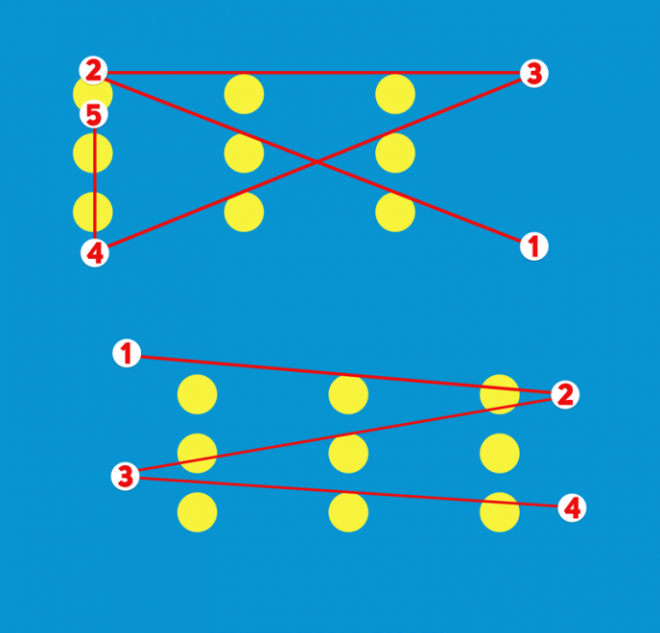
Когда вы соединили первые восемь точек фигуры четырьмя линиями, осталось только завершить обход, соединив последнюю, девятую точку, с исходной. На первый взгляд может показаться, что это невозможно, так как для этого придется пройти по уже проведенным линиям. Но существует несколько методов, позволяющих успешно завершить обход в исходной вершине.

Один из таких методов предполагает проведение перпендикулярной линии от последней точки к одной из предыдущих линий, и затем соединение этой точки с исходной вершиной. Для этого необходимо провести аккуратно перпендикулярную линию, чтобы она не пересекала другие линии. Этот метод может требовать точности и аккуратности, так как нужно выбирать правильную точку для соединения, чтобы исходная вершина оказалась «связанной» с остальными точками.

Другим методом является использование «дырки» внутри фигуры. Для этого можно провести одну из линий через внутреннюю область фигуры, таким образом, чтобы в итоге она оказалась соединена с исходной вершиной. Этот метод может выглядеть необычно, но при правильном планировании и проведении линий, можно добиться нужного результата.