Как соединить девять точек всего четырьмя линиями

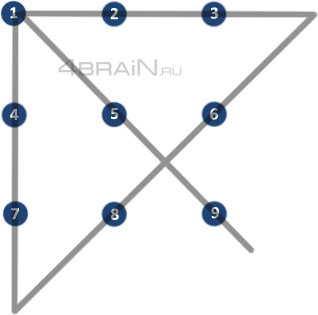
Видение геометрических фигур и их взаимодействия часто требует способности мыслить нестандартно. Одна из таких задач связана с соединением девяти точек четырьмя прямыми линиями.

Данная задача была впервые описана Андрианом Паскалем в 1659 году в его труде «Трактат о шариковых играх». Паскаль предложил решение для подобного случая, и оно до сих пор вызывает интерес и удивление своей простотой и неожиданностью.

Для решения этой задачи необходимо использовать основные принципы геометрии и творческого мышления. Подход, предложенный Паскалем, показывает, что для соединения девяти точек всего четырьмя линиями нужно мыслить трехмерно и использовать нестандартные ходы.

Секрет успешного соединения девяти точек четырьмя линиями

Задача соединения девяти точек всего четырьмя линиями может показаться сложной, но на самом деле имеет свой секрет успеха. Во-первых, необходимо проявить творческий подход к решению задачи. Узколобый образ мышления может быть помехой в достижении цели.

Во-вторых, важно учесть, что линии не обязаны быть прямыми. Допускается их изгиб и комбинирование, что значительно расширяет варианты решения задачи. Иногда тот, кто думает нестандартно, может обнаружить решение, которое другие даже не заметят.

В-третьих, нужно использовать логику и аналитический подход к задаче. Разобравшись в связях между точками и определив возможные варианты соединения, можно создать план действий. Важно не спешить, а внимательно анализировать каждое действие и его возможные последствия.

Следует также отметить, что успешное соединение девяти точек четырьмя линиями требует умения замечать детали. Некоторые действия могут быть незаметными на первый взгляд, но важными для общего результата. Умение видеть большую картину и мелкие элементы поможет достичь успеха.

Наконец, не стоит бояться ошибиться или пойти нестандартным путем. Иногда именно из ошибок рождаются новые идеи и решения. Важно сохранять наработки, даже если они не привели к желаемому результату. Неуверенность и страх не помогут достигнуть цели, а только будут стоять на пути к успеху.

В итоге, соединение девяти точек четырьмя линиями требует творческого подхода, аналитического мышления, внимания к деталям и готовности к нестандартным решениям. Возможные варианты решения могут быть разными, но важно сохранять уверенность в достижении цели и не останавливаться перед трудностями.

Почему так сложно?

Решить задачу о соединении девяти точек всего четырьмя линиями оказывается не так просто, как может показаться на первый взгляд. Данная задача представляет интерес для многих математиков и ученых, так как она требует тщательного анализа и поиска нестандартных решений.

Одной из причин, по которой задача сложна, является ограничение на количество линий, которыми можно соединять точки. В данной задаче допустимо использовать только четыре линии, что накладывает определенные ограничения на возможные варианты решений.

Кроме того, важным аспектом сложности задачи является необходимость прохождения через все девять точек. Это означает, что каждая из линий должна проходить через определенные точки, и при этом не должна пересекаться с другими линиями. Такие ограничения делают решение задачи еще более запутанным.

Также стоит отметить, что решение данной задачи требует креативности и умения мыслить нестандартно. Часто для ее решения необходимо представить исходные данные в новом свете и обратить внимание на некоторые скрытые особенности. Это тест на логику и интуицию, который ставит перед нами отличную возможность для развития критического мышления и нахождения необычных решений.

Определение задачи

Задача «Как соединить девять точек всего четырьмя линиями» представляет собой головоломку, которая требует от решателя найти способ соединить все девять точек, проведя только четыре линии без отрыва карандаша от бумаги.

Данная задача проверяет умение распознавать образы и находить нестандартные решения. Решение должно быть логически обоснованным и представлять собой последовательность действий, в результате которой все точки будут соединены.

Задача активно использует мыслительные процессы, связанные с пространственным восприятием, представлением образов и поиском альтернативных путей. Решение требует гибкости мышления и способности мысленно манипулировать объектами.

Одним из возможных вариантов решения данной задачи является применение графовых алгоритмов, которые позволяют находить оптимальные пути и связи между элементами. Также возможно решение задачи путем разделения всех точек на группы и последовательного соединения точек внутри каждой группы и между группами.

Что такое «точка»?

Точка — это абстрактное понятие, используемое в математике и геометрии для обозначения маленького объекта без размеров или объема. Точка не имеет никаких измерений, она не имеет ни длины, ни ширины, ни высоты. Можно представить точку как некий «маркер» или «отметку» на плоскости или в пространстве.

В контексте графического представления точка обычно обозначается кругом или небольшим квадратом. Точка может быть представлена с помощью своих координат — чисел, определяющих ее положение на плоскости или в пространстве. В двумерном пространстве точка имеет две координаты — абсциссу и ординату, а в трехмерном — еще и ординату.

Точки могут быть использованы для создания геометрических фигур, линий, отрезков и других объектов. Они играют важную роль в науке, инженерии и визуальном искусстве. Точки используются для определения расстояний, углов, форм и размеров. Они также являются основным строительным блоком в графических программах и дизайне, где они помогают создавать изображения и пространственные композиции.

Что такое «линия»?

Линия — это геометрическая фигура, которая представляет собой бесконечно тонкую и прямую образующую. Она не имеет толщины и может быть задана точками или уравнением.

Линии находят широкое применение в геометрии, а также во многих других областях, таких как физика, инженерия и компьютерная графика. В геометрии, линии используются для определения границы между двумя точками или для указания направления движения.

Существует несколько типов линий, включая прямую линию, кривую линию, замкнутую линию, ломаную линию и другие. Прямая линия является самой простой формой линии и представляет собой наиболее короткое расстояние между двумя точками.

Строительство линий может быть достаточно сложным заданием, особенно при необходимости соединить несколько точек всего небольшим количеством линий. Однако, с помощью определенных методов и подходов, таких как использование коротких дуг или меньшее количество прямых, это возможно выполнить.

• Линия — геометрическая фигура, обладающая нулевой толщиной и прямолинейной формой.
• Линии используются для определения границы между точками и указания направления движения.
• Существуют различные типы линий, включая прямую, кривую и замкнутую.
• При соединении нескольких точек ограниченным количеством линий следует использовать определенные методы и приемы.

Ключевые этапы решения

1. Знакомство с задачей: В первую очередь нужно понять, что требуется соединить все девять точек всего лишь четырьмя линиями. Изучите условие задачи и уясните ограничения.

2. Анализ задачи: Проанализируйте графическое представление задачи и выделите особенности, которые помогут вам найти решение.

3. Поиск возможных вариантов: Используйте логическое мышление и экспериментируйте с различными способами соединения точек. Рассмотрите все возможные комбинации и варианты.

4. Выбор оптимального решения: Отберите наиболее подходящий вариант из представленных, который соответствует условиям задачи и позволяет соединить все девять точек всего четырьмя линиями.

5. Проверка решения: Проверьте, соответствует ли ваше выбранное решение условиям задачи и действительно позволяет соединить все девять точек. Если решение верное, то переходите к следующему шагу. В противном случае, возвращайтесь к предыдущим этапам и ищите альтернативные решения.

6. Формализация решения: Опишите свое решение в формальном виде, используя символы, графические обозначения или математические формулы. Это поможет ясно и однозначно представить ваш подход к решению задачи.

7. Доказательство корректности решения: Продемонстрируйте, что ваше выбранное решение действительно может быть выполнено согласно условиям задачи. Предоставьте логическое объяснение и доказательство для этого.

Как найти точки?

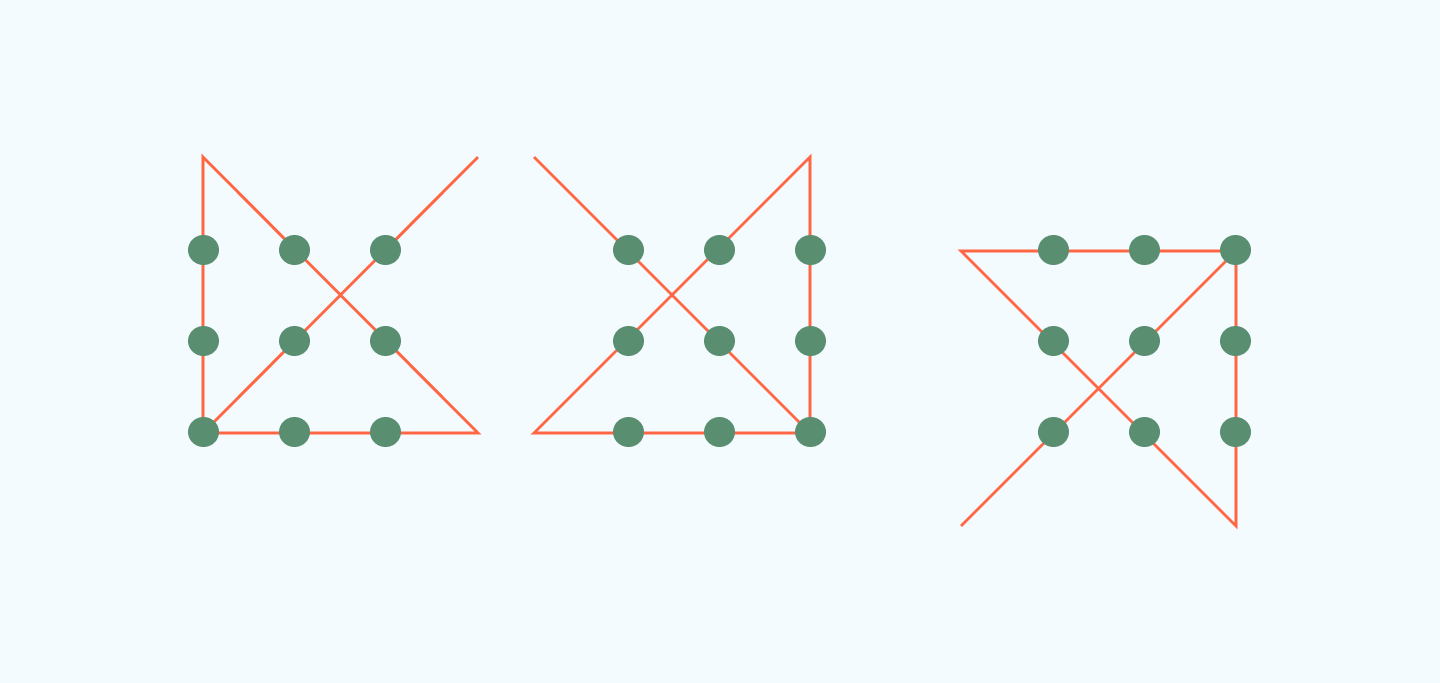
Для того чтобы найти все девять точек в задаче соединения четырьмя линиями, необходимо использовать систематический подход.

Первым шагом является нахождение начальной точки, расположенной в центре. Далее, нужно найти четыре точки, которые расположены на углах прямоугольника. Эти точки представляют собой часть границы и представляются более явно.

Вторым шагом является нахождение пяти оставшихся точек. Эти точки должны быть расположены на прямых линиях, которые соединяют внутренние углы границы прямоугольника. Важно помнить, что эти точки не являются вершинами прямоугольника и могут быть найдены только на прямых линиях.

Выберите одну из оставшихся точек и соедините ее с начальной точкой. Таким образом, будет получена первая линия. Затем, выберите следующую точку и соедините ее с любой другой точкой, которая еще не была связана линией. Продолжайте этот процесс до тех пор, пока все точки не будут соединены четырьмя линиями.

Как провести линии?

Для того чтобы соединить девять точек всего четырьмя линиями, необходимо следовать определенным правилам. Первым шагом является выбор точки, с которой начать проведение линий. Важно выбрать такую точку, которая позволит провести линии через другие точки.

Затем нужно выбрать направление, в котором будут проведены линии. Это также важно, чтобы линии не пересекались и чтобы все точки были соединены. Чтобы линии не пересекались, можно использовать геометрические принципы, такие как пересечение линий под определенным углом.

Еще одним способом проведения линий является использование сетки из точек. Для этого можно нарисовать квадратную сетку из точек и провести линии через эти точки. Важно выбрать такие точки, чтобы линии формировали геометрическую фигуру.

Кроме того, можно использовать математические формулы для проведения линий через точки. Например, можно использовать уравнение прямой для расчета координат точек, через которые должны проходить линии.

Как проверить соединение?

Проверка соединения — это одна из важнейших задач при работе с компьютерными сетями. Существует несколько способов проверить соединение и убедиться, что все работает должным образом.

Первый способ — пинг. Команда ping используется для проверки связи между двумя узлами сети. При этом отправляются небольшие пакеты данных, и затем проверяется, успешно ли они были получены. Если ответы от удаленного узла получены успешно, это означает, что соединение работает нормально.

Второй способ — тестирование порта. При тестировании порта отправляется запрос на определенный порт удаленного узла. Если удаленный узел отвечает, это означает, что порт открыт и соединение может быть установлено. Этот способ позволяет проверить доступность конкретного сервиса или приложения.

Третий способ — использование утилиты tracert. Команда tracert позволяет отслеживать маршрут следования пакетов данных от отправителя до получателя. Это помогает идентифицировать возможные проблемы сети, такие как узкие места или задержки, и выявить точку отказа.

Четвертый способ — использование сетевого анализатора. Сетевой анализатор позволяет исследовать трафик в сети и выявлять возможные проблемы. Он анализирует данные, перехваченные на определенных уровнях сетевой структуры, и предоставляет информацию о скорости передачи данных, потере пакетов, задержке и других параметрах. Это помогает определить, где именно возникают проблемы соединения.

В завершение, необходимо помнить, что проверка соединения должна проводиться регулярно, особенно при работе с критически важными системами. Это поможет выявить и устранить возможные проблемы связи, обеспечивая бесперебойную работу сети.

Советы и рекомендации

Для того чтобы успешно соединить девять точек всего четырьмя линиями, следует придерживаться нескольких советов и рекомендаций.

Во-первых, учтите, что одна линия может проходить через несколько точек. Это означает, что при прокладке линий не следует ограничиваться только одной точкой. Используйте дополнительные точки, чтобы создать более сложные и интересные линии.

Во-вторых, экспериментируйте с направлением линий. Вместо прямых линий попробуйте создать изогнутые или даже вьющиеся линии. Такие линии могут добавить динамизма и интереса в решении головоломки.

Еще одним полезным советом является использование фигур и образов для прокладки линий. Например, можно создать треугольник или квадрат, используя три или четыре точки, и затем соединить оставшиеся точки.

Не стесняйтесь использовать различные цвета линий для создания контраста и выделения. Это поможет сделать головоломку более наглядной и интересной для решения.

Важным аспектом при решении такой головоломки является порядок соединения точек. Старайтесь соединять точки таким образом, чтобы линии не пересекались и не пересекали другие линии. Это поможет создать четыре различных линии и решить головоломку по условию.

Используйте решетку

Одним из эффективных способов решить головоломку «Как соединить девять точек всего четырьмя линиями» является использование решетки. Решетка — это сетка из квадратных ячеек, которая позволяет легко визуализировать и передвигать точки.

Подходящая стратегия заключается в том, чтобы начать соединять точки, используя только горизонтальные и вертикальные линии. Затем, если это необходимо, можно использовать диагональные линии.

С помощью решетки можно легко находить оптимальные пути для соединения точек. Можно прокладывать пути по горизонтали и вертикали, сокращая количество необходимых линий и создавая более эстетически приятное решение.

Для наглядности можно использовать разные цвета линий или разные стили линий. Например, можно использовать пунктирные линии или толстые линии для выделения главного пути.

Помечайте точки и линии

Чтобы успешно соединить девять точек всего четырьмя линиями, вам потребуется умение правильно помечать точки и линии. Во-первых, отметьте все девять точек на листе бумаги или в программе для рисования. Это поможет вам визуализировать задачу и понять, как они расположены.

Далее, обведите точки кругом или пронумеруйте их, чтобы легче было ориентироваться. Вы можете использовать цифры или буквы в качестве меток точек. Главное — чтобы вы могли упорядочить точки и не запутаться.

После того как точки будут помечены, перейдите к отметке линий. Вам потребуется провести четыре линии, чтобы соединить все девять точек. Начинайте с одной точки и прокладывайте линию через другие точки, пока не достигнете следующей помеченной точки.

Используйте разные типы линий, чтобы обозначить соединения между точками. Вы можете использовать сплошные линии, пунктирные линии или любые другие стили, чтобы подчеркнуть связи между точками.

Проверяйте соединение после каждого шага

Когда вы пытаетесь соединить девять точек всего четырьмя линиями, важно проверять соединение после каждого шага. Это позволит вам убедиться, что вы на правильном пути и не допустили ошибок. Проверка соединения поможет вам найти возможные проблемы и внести необходимые корректировки.

Для проведения проверки, внимательно просмотрите каждую линию, удостоверьтесь, что она правильно соединена с нужными точками. Используйте видео или фотофиксацию, чтобы убедиться, что каждое соединение ясно и четко видно. Если вы заметили ошибку или несоответствие, вернитесь к предыдущим шагам и проверьте точность ваших движений.

Проверка соединения после каждого шага поможет вам эффективно следить за прогрессом и найти возможные ошибки в процессе. Она также поможет вам учиться на своих ошибках и становиться лучше в решении подобных задач. Без проверки вы рискуете потерять много времени и энергии на возвращение к предыдущим шагам и исправление ошибок.