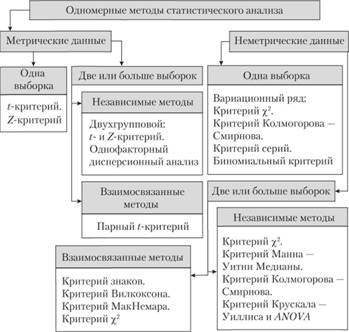
Статистический анализ данных – это процесс сбора, организации, анализа и интерпретации данных с целью извлечения информации и понимания характеристик, связей и трендов. Он является неотъемлемой частью современного исследования и представляет собой мощный инструмент для принятия информированных решений.
Однако, выбор правильных методов статистического анализа данных – это сложная задача, требующая знаний и опыта. В зависимости от типа данных, цели исследования и особенностей выборки могут быть использованы различные подходы. В данной статье мы рассмотрим некоторые из лучших методов статистического анализа данных, которые могут быть применены в различных областях исследования.
Один из наиболее часто используемых методов статистического анализа данных – это дескриптивная статистика. Она включает в себя описание основных характеристик данных, таких как среднее значение, медиана, стандартное отклонение и т.д. Дескриптивная статистика позволяет получить первичное представление о данных и определить их основные свойства и распределение.
Методы множественной регрессии
Методы множественной регрессии являются одними из наиболее распространенных и эффективных подходов в статистическом анализе данных. Они позволяют моделировать зависимость одной переменной от нескольких независимых переменных, учитывая их влияние на исследуемый процесс.
В основе методов множественной регрессии лежит линейная модель, которая предполагает линейную зависимость между зависимой переменной и независимыми переменными. Однако, методы множественной регрессии позволяют учесть и нелинейные зависимости, используя различные трансформации переменных или включая в модель полиномиальные члены.
Основным понятием при использовании методов множественной регрессии является понятие коэффициента регрессии. Этот коэффициент показывает, насколько изменяется зависимая переменная при изменении одной единицы независимой переменной, при условии, что остальные переменные остаются постоянными.
Для определения коэффициентов регрессии в методах множественной регрессии используется метод наименьших квадратов, который минимизирует сумму квадратов отклонений между наблюдаемыми и предсказанными значениями зависимой переменной. Таким образом, методы множественной регрессии позволяют наилучшим образом описать зависимость между переменными и прогнозировать значения зависимой переменной на основе независимых переменных.
Определение и принцип работы
Статистический анализ данных — это методология изучения данных, основанная на применении статистических методов и техник для извлечения информации, получения выводов и принятия решений. Он используется в различных областях, таких как бизнес, медицина, наука и т.д., для анализа и интерпретации больших объемов данных.
Принцип работы статистического анализа данных заключается в следующих этапах:
- Сбор данных. На этом этапе происходит сбор и накопление данных, которые подлежат анализу. Это может быть проведение опросов, наблюдение, эксперименты или использование доступных баз данных.
- Очистка данных. После сбора данных следует их очистка от ошибок, выбросов и пропущенных значений. Это важный шаг, поскольку качество и точность анализа зависит от качества данных.
- Описательная статистика. Далее проводится анализ данных, используя методы описательной статистики. Она помогает описать основные характеристики данных, такие как среднее значение, медиана, дисперсия и т.д. Это помогает получить первичное представление о данных и выявить особенности в их распределении.
- Статистические тесты. После описательного анализа следует применение статистических тестов для проверки гипотез и выявления статистической значимости. Это может быть t-тест, ANOVA, корреляционный анализ и др.
- Выводы и интерпретация. На последнем этапе проводится интерпретация результатов и делаются выводы на основе статистического анализа данных. Это позволяет принимать обоснованные решения и предлагать рекомендации на основе имеющихся данных.
Таким образом, статистический анализ данных играет важную роль в процессе принятия решений, и его правильное выполнение способствует более точному и эффективному использованию информации, содержащейся в данных.
Преимущества и ограничения метода
Метод статистического анализа данных имеет некоторые преимущества, которые делают его важным инструментом при исследовании и анализе данных. Во-первых, метод позволяет обрабатывать большие объемы данных и находить в них закономерности и структуру. Это особенно полезно для компаний и организаций, которые хранят и обрабатывают большие массивы информации.
Во-вторых, метод статистического анализа данных позволяет проводить объективное и надежное исследование. Он основывается на математических принципах и правилах, что позволяет устранить субъективность и ошибки, связанные с человеческим фактором.
Однако метод статистического анализа данных также имеет свои ограничения. Во-первых, для его применения требуется достаточно большое количество данных. Если данных недостаточно, то результаты анализа могут быть неточными и недостоверными.
Во-вторых, метод статистического анализа данных может быть сложным и требовать определенных знаний и навыков. Не все исследователи и аналитики могут владеть этими методами, что может стать препятствием для их использования.
Также, метод статистического анализа данных не может давать точные и окончательные ответы на все вопросы. Он может только предоставить статистические выводы и предположения, которые требуют последующей интерпретации и анализа.
Анализ дисперсии
Анализ дисперсии (ANOVA) — это статистический метод, который позволяет сравнивать средние значения нескольких групп или образцов и определять, есть ли статистически значимые различия между ними. Он является одним из основных инструментов в статистическом анализе данных и широко применяется в различных областях, включая экспериментальную психологию, биологию, экономику и маркетинг.
Основная идея анализа дисперсии заключается в разбиении общей дисперсии данных на две составляющие: внутригрупповую дисперсию и межгрупповую дисперсию. Внутригрупповая дисперсия отражает разброс значений внутри каждой группы, а межгрупповая дисперсия отражает различия между средними значениями групп.
Для проведения анализа дисперсии необходимо выполнить следующие шаги:
- Сформулировать нулевую и альтернативную гипотезы. Нулевая гипотеза заключается в отсутствии различий между группами, а альтернативная гипотеза — в наличии различий.
- Выбрать уровень значимости, который определяет, насколько сильные должны быть различия между группами, чтобы отвергнуть нулевую гипотезу.
- Провести статистический анализ данных, используя соответствующие статистические тесты.
- Интерпретировать полученные результаты и сделать выводы о наличии или отсутствии статистически значимых различий между группами.
Анализ дисперсии имеет несколько вариаций, включая однофакторный ANOVA, многофакторный ANOVA и дисперсионный анализ с повторными измерениями. Каждая из этих вариаций предназначена для определенных ситуаций и требует соответствующих статистических моделей и методов.
В заключение можно сказать, что анализ дисперсии является мощным инструментом статистического анализа данных, который позволяет выявлять значимые различия между группами и проводить сравнительный анализ. Он позволяет исследователям сделать более обоснованные выводы на основе данных и принять обоснованные решения.
Определение и цель анализа дисперсии

Анализ дисперсии — это метод статистического анализа данных, который используется для изучения различий между несколькими группами или образцами. Он позволяет определить, насколько вариабельны значения внутри группы и между группами, и выявить наличие статистически значимых различий.
Основная цель анализа дисперсии — установить, есть ли статистически значимые различия между средними значениями в разных группах. Например, можно использовать этот метод, чтобы проверить эффективность разных лекарственных препаратов или сравнить продуктивность разных методов обучения.
При проведении анализа дисперсии, данные разбиваются на группы в соответствии с независимыми переменными, и вычисляются средние значения по каждой группе. Затем определяется общая дисперсия, то есть мера рассеивания данных во всех группах, и внутригрупповая дисперсия, то есть мера рассеивания данных внутри каждой группы.
Далее с помощью статистических тестов, например, F-теста, проверяется статистическая значимость различий между средними значениями в группах. Если полученное значение F-статистики превышает критическое значение, то можно сделать вывод о наличии статистически значимых различий между группами.
Расчет F-критерия и интерпретация результатов

Расчет F-критерия — основной шаг в анализе дисперсии и сравнении средних значений между группами. Данный критерий позволяет оценить, является ли различие между группами статистически значимым или возникло случайно.
Применение F-критерия требует выполнения нескольких условий, включая однородность дисперсий. Поэтому перед расчетом F-критерия рекомендуется проверить выполнение этих условий с помощью других статистических тестов, таких как тест Левена или тест Бартлетта. Если условия выполнены, можно приступать к расчету F-критерия.
Расчет F-критерия основан на сравнении дисперсии между группами с общей внутригрупповой дисперсией. Для этого рассчитывается значение F-статистики, которое представляет собой отношение межгрупповой суммы квадратов к внутригрупповой сумме квадратов. Чем больше значение F-статистики, тем более различны группы между собой.
После расчета F-статистики производится интерпретация результатов. Для этого сравнивают полученное значение F-критерия с критическим значением, которое зависит от выбранного уровня значимости и числа степеней свободы. Если значение F-критерия превышает критическое значение, то различия между группами статистически значимы. В противном случае, различия считаются незначимыми.
Кластерный анализ
Кластерный анализ — это метод статистического анализа данных, который используется для группировки объектов или переменных в отдельные кластеры на основе их сходства. Он помогает выявить скрытые структуры в данных, обнаружить группы схожих объектов и сделать выводы на основе этих групп.
Кластерный анализ часто используется в маркетинге, социологии, биологии, медицине и других областях, где необходимо провести сегментацию или классификацию данных. Он также может быть полезен при анализе больших объемов информации, когда необходимо выявить общие особенности множества объектов.
Существует несколько основных методов кластерного анализа, включая иерархический и непараметрический методы. В иерархическом методе объекты группируются на основе их сходства, путем последовательного объединения или разделения кластеров. Непараметрический метод кластерного анализа, такой как K-средних или DBSCAN, использует математические алгоритмы для выделения кластеров.
При проведении кластерного анализа необходимо определить, какие переменные будут использоваться для группировки объектов, каким образом будет измеряться сходство между объектами и каким образом будут определены и объяснены обнаруженные кластеры. Также важно учитывать особенности данных, такие как выбросы или отсутствие значений.
В результате кластерного анализа можно получить набор кластеров, в которых объекты схожи между собой, а отличаются от объектов в других кластерах. Это может помочь в понимании структуры данных, выявлении сегментов или типов объектов, а также в создании моделей или принятии решений на основе этих кластеров.
Определение и применение кластерного анализа

Кластерный анализ представляет собой статистический метод, используемый для классификации данных и выявления скрытых закономерностей в больших объемах информации. Он позволяет группировать схожие объекты в отдельные кластеры на основе их сходства и различия. Кластерный анализ находит широкое применение в различных областях, включая маркетинг, медицину, социологию, экономику и компьютерные науки.
Применение кластерного анализа позволяет проводить сегментацию аудитории или рынка, идентифицируя группы схожих потребителей или товаров. Это помогает компаниям эффективнее планировать свои рекламные кампании, разрабатывать персонализированные предложения и добиваться большей конверсии. Кроме того, кластерный анализ может быть использован для выявления подгрупп пациентов схожего риска заболевания или для классификации клиентов банковских учреждений.
В кластерном анализе существуют различные методы и алгоритмы, позволяющие проводить кластеризацию данных. Некоторые из них базируются на определении расстояния между объектами, такие как иерархическая кластеризация или метод k-средних. Другие методы, такие как алгоритм DBSCAN или EM-алгоритм, учитывают плотность распределения объектов. Выбор конкретного метода зависит от характеристик исходных данных и целей исследования.
Использование кластерного анализа позволяет упростить сложные наборы данных и выявить скрытую структуру, что может помочь в принятии более обоснованных решений. К этому методу стоит обратиться при анализе больших объемов информации, когда необходимо систематизировать данные и найти общие закономерности среди множества различных объектов.
Выбор меры близости и алгоритма кластеризации
Меры близости и алгоритмы кластеризации являются ключевыми компонентами в статистическом анализе данных. Выбор правильной меры близости и алгоритма кластеризации может существенно повлиять на результаты кластерного анализа.
Важно учитывать природу данных и цели исследования при выборе меры близости и алгоритма кластеризации. Например, если данные представляют собой числовые величины, то может быть полезно использовать евклидово расстояние или косинусную меру близости. Если данные представляют собой категориальные переменные, то можно использовать меру Жаккара или коэффициент Юста.
Для выбора алгоритма кластеризации также необходимо учитывать различные факторы, такие как размер данных, форма кластеров, наличие шума и выбросов. Некоторые из наиболее популярных алгоритмов кластеризации включают k-средних, DBSCAN и иерархическую кластеризацию. Каждый из них имеет свои преимущества и недостатки, и их выбор зависит от конкретных условий.
При выборе меры близости и алгоритма кластеризации необходимо проводить эксперименты и тестирование для оценки качества кластерного анализа и сравнения различных подходов. Такой подход поможет выбрать наиболее подходящую меру близости и алгоритм кластеризации для решения конкретной задачи статистического анализа данных.








