
Неявные определения представляют собой особую форму выражения, где мы понимаем значение понятия, но не можем явно дать точное определение. Такие определения играют важную роль в логике, поскольку позволяют нам оперировать общими понятиями и идеями, не задавая им конкретных границ и условий.
Принцип работы неявных определений основан на использовании контекста и семантики высказывания. Часто они используются для описания сложных и абстрактных понятий, которые трудно представить в явном виде. Неявные определения помогают нам понять суть и смысл таких понятий, не утверждая их конкретными словами, а используя определенные связи с другими понятиями или идеями.
Примером неявного определения может служить понятие «счастье». Мы все имеем представление о том, что такое счастье, но его точное определение оказывается довольно сложным. Вместо того, чтобы пытаться описать счастье словами, мы можем использовать неявное определение и связать это понятие с другими, например, с любовью, успехом или душевным равновесием.
Неявные определения широко применяются в логике, философии и науке. Они помогают нам описывать и понимать сложные концепты, которые не всегда могут быть выражены четко и явно. Использование неявных определений позволяет нам глубже проникнуть в суть вещей и интерпретировать их контекстуально, открывая новые понимания и выводы.
Определение неявности

Неявность в логике относится к понятию, которое не явно или неявно определено в тексте высказывания или аргументации. Она может быть связана с необходимостью предположений, которые не явно указаны, но считаются подразумеваемыми в контексте.
Неявные определения являются важным уровнем логического анализа текстов и помогают раскрыть скрытые предположения, которые влияют на доказательства и выводы. Они могут включать логические правила, значения терминов или факты, которые авторы предполагают известными читателю.
Отсутствие явного определения может привести к неоднозначности и недостаточной ясности в аргументации. Поэтому важно распознавать и анализировать неявные определения, чтобы получить полное понимание контекста и сделать точные логические выводы.
Неявные определения могут быть выявлены путем внимательного анализа текста, выявления доступной информации и разбора содержательных аргументов. Это помогает избежать логических ошибок, противоречий и недостаточных логических выводов в процессе дедукции и анализа.
Исторический контекст
Разработка логических принципов и правил играла значительную роль в философии и математике с древних времен. В древнем Востоке, например, в Индии и Китае, были созданы системы логических законов, которые определяли правильное мышление и рассуждения.
В Западной философии развитие формальной логики началось в Греции. Сократ, Платон и Аристотель разработали основные принципы логического мышления и методы для построения аргументации. Их работы впоследствии оказали существенное влияние на развитие логики и научного метода в Европе в средние века и Новое время.
Важный вклад в развитие логического мышления внесли также философы и математики эпохи Просвещения, среди которых выделяются Лейбниц, Кант и Гегель. Они разработали новые методы логического мышления и подходы к формализации рассуждений.
В начале XX века логика претерпела революцию благодаря появлению математической логики. Математики, в том числе Нильс Бор, Дэвид Гильберт, Алонзо Чёрч и Алан Тьюринг, разработали формальные системы логики и аксиоматику, которые стали основой для создания компьютеров и искусственного интеллекта.
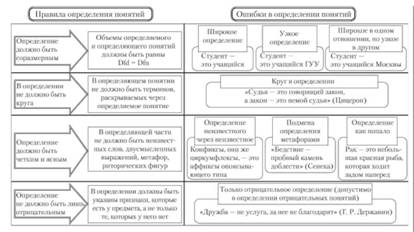
Принципы неявных определений
1. Конкретность: Определение должно быть ясным и однозначным, чтобы не вызывать недоразумений и разночтений. Неявные определения должны быть предметными и конкретными, чтобы избежать размытости и неопределенности в их интерпретации.
2. Контекстуальность: Неявные определения должны учитывать контекст, в котором они используются. Многозначность может возникнуть из-за разных контекстов, поэтому необходимо принимать во внимание окружение и обстоятельства, в которых происходит употребление определения.
3. Список отношений: Определение может включать в себя список связанных понятий или отношений, чтобы дать более полное представление о его значении. Это может помочь уточнить и расширить его смысл, а также установить связи между различными понятиями.
4. Логическое следование: Определение должно быть логически связанным с определяющим понятием. Оно должно следовать из основной идеи или сути определяемого понятия, чтобы не вызывать противоречий или непонимания.
5. Ясность и краткость: Неявные определения должны быть ясными и лаконичными, чтобы не перегружать текст излишней информацией. Они должны быть выражены в достаточной мере, чтобы передать необходимую суть, но при этом быть краткими и легко запоминающимися.
6. Доступность: Определение должно быть доступным для понимания широкого круга лиц. Оно не должно содержать сложные термины или специфическую терминологию, которая может быть непонятна для обычных пользователей. Оно должно быть сформулировано простым и понятным языком.
7. Источники и авторитетность: Неявные определения должны быть основаны на достоверных и авторитетных источниках. Они должны быть подкреплены доказательствами и ссылками на исследования, эксперименты или другие источники информации. Такие определения имеют большую степень надежности и весомости.
Принцип суждений
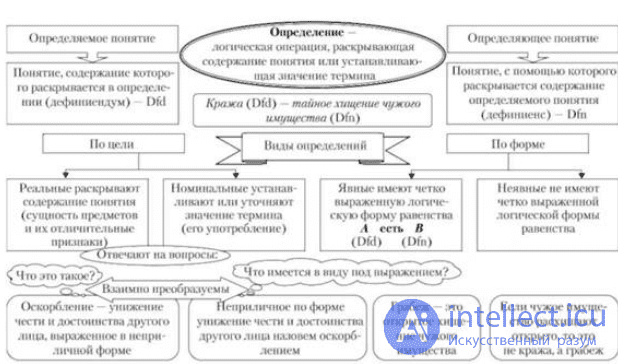
Принцип суждений является фундаментальным принципом в логике и философии. Он утверждает, что все высказывания, предположения или утверждения должны быть явно или неявно суждениями. Суждение — это выражение, которое имеет истинностное значение и может быть истинным или ложным.
Принцип суждений важен, чтобы ясно и однозначно определять содержание высказывания и его истинностное значение. Суждение имеет форму «A есть B» или «A характеристика B» и используется для выражения отношений между объектами или свойствами мира.
Примеры суждений могут быть: «Солнце светит», «Морская вода соленая», «Мясо красное». Все эти высказывания содержат суждения о фактах или свойствах.
Принцип суждений позволяет нам анализировать и оценивать высказывания с точки зрения их истинности или ложности. Он является основой для построения логических выводов и аргументаций.
Принцип суждений также связан с понятием квази-суждений, которые содержат в себе неявные суждения. Квази-суждение — это выражение, которое содержит в себе неявное суждение, например, «Погода хорошая», где предполагается неявное суждение «Солнце светит».
В целом, принцип суждений является фундаментальным принципом в логике и философии, он помогает нам определять и анализировать высказывания, основываясь на их суждениях и истинности.
Принцип предикатов
Принцип предикатов является одним из основных принципов в логике и используется для определения и описания свойств и качеств объектов. Предикаты — это выражения, которые связывают объекты с определенными свойствами или отношениями.
Принцип предикатов гласит, что для описания любого объекта или явления мы можем использовать предикаты, которые устанавливают какие-либо свойства или отношения между объектами. Предикаты могут быть простыми или составными, и они определяются с помощью логических операторов и кванторов.
Одним из примеров принципа предикатов является так называемое «кванторное определение». Например, мы можем определить понятие «студент» с помощью предиката «учится в университете». Таким образом, мы можем сказать, что «студент — это человек, который учится в университете». Здесь предикат «учится в университете» связывает объект «студент» с его свойством «учиться в университете».
Принцип предикатов позволяет нам более точно и ясно описывать объекты и явления с помощью логических конструкций. Он является одним из основных инструментов логики и используется в различных областях знания, таких как математика, философия, компьютерная наука и др.
Примеры неявных определений
Неявные определения в логике имеют множество примеров, которые могут быть полезными для понимания и применения этого концепта. Одним из примеров является ситуация, когда мы говорим о классическом примере овоща — моркови. Мы можем применить неявное определение, чтобы объяснить, что морковь — это овощ, который широко используется в кулинарии и содержит много витаминов и питательных веществ.
Другим примером является определение цвета. Мы можем сказать, что синий — это цвет, который ассоциируется с небом или морем, без явного указания причины этой ассоциации. Это неявное определение позволяет нам понять цвет синий и использовать его в контексте различных областей, таких как дизайн или искусство.
Еще одним примером неявного определения может быть обсуждение понятия «дружба». Мы можем сказать, что дружба — это отношение, основанное на взаимной привязанности, доверии и поддержке, без ссылки на конкретные действия или ситуации. Это позволяет нам понять, что дружба может проявляться по-разному в различных ситуациях, но иметь общие основы и характеристики.
Для наглядности можно привести еще один пример неявного определения, связанный с понятием «успех». Мы можем сказать, что успех — это достижение поставленных целей и выполнение задач, без указания конкретной сферы жизни или критериев успеха. Это позволяет нам понимать, что успех может быть разным для разных людей и зависеть от их индивидуальных целей и ценностей.
Неявное определение в математике

В математике существует понятие неявного определения, которое используется для задания объектов или свойств без явного указания их характеристик. Неявное определение позволяет описывать объекты или отношения на основе некоторых свойств или условий, которые могут быть неявно предположены.
Одним из примеров неявного определения в математике является уравнение эллипса. Уравнение эллипса задается в виде: x2/a2 + y2/b2 = 1, где a и b являются полуосями эллипса. В данном случае, объектом является эллипс, а его характеристики (полуоси) не указываются явно, а задаются через уравнение.
Другим примером неявного определения является определение функции как отображения, которое может быть записано следующим образом: f: X -> Y, где X — множество аргументов (область определения), Y — множество значений (область значений). В данном случае, объектом является функция, а её характеристики (аргументы и значения) не указываются явно, а задаются через обозначение отображения.
Неявное определение в математике широко используется для описания различных объектов и отношений, а также для формулировки условий и свойств. Такое определение позволяет более гибко описывать математические объекты и рассматривать их различные свойства без явного указания всех характеристик.
Неявное определение в философии
Неявное определение, одно из ключевых понятий в философии, является основой для анализа истинности утверждений и понятий. Оно предполагает скрытое или подразумеваемое определение, которое не является явным или ясным для всех. Неявные определения могут быть неявными связями или предпосылками, которые не упоминаются напрямую, но при этом влияют на наше понимание и оценку концепта или аргумента.
Принцип неявного определения в философии заключается в том, что для полного и точного понимания какого-либо понятия или идеи необходимо учитывать не только явные определения, но и скрытые возможности, которые могут влиять на их смысл и интерпретацию. Важно осознавать, что неявные определения могут быть неоднозначными и различными для разных людей и культур.
Примером неявного определения в философии может служить понятие «свобода». Вроде бы это простое и понятное понятие, но оно имеет много разных трактовок. Каждый человек может воспринимать свободу по-своему, иметь свои неявные представления о том, что значит быть свободным. Эти неявные представления могут проистекать из предыдущего жизненного опыта, культурных норм или субъективных ожиданий. Поэтому, при обсуждении свободы, необходимо учесть и неявные определения, чтобы полноценно понять, о чем идет речь.
Раскрытие неявных определений является важным инструментом в философии, помогающим более глубоко понять, анализировать и критически оценивать концепты и аргументы. Благодаря разбору неявных определений, мы можем расширить свое понимание и быть более гибкими в интерпретации различных философских понятий.








