Логика как наука об умозаключениях и доказательствах ведет свое начало от древних греков, однако, несмотря на свою богатую историю и бесчисленное количество разработанных правил и принципов, логика все равно имеет свои противоречия и парадоксы. Один из таких парадоксов — это пара противоречивых утверждений, которые, несмотря на свою логическую недостоверность, все равно обладают определенной логической последовательностью.
Парадоксальность логических утверждений проявляется в их взаимном противоречии и непоследовательности, что выглядит как логическая абсурдность. Как правило, в таких случаях можно найти ошибку в логическом рассуждении или предпосылке, однако, в случае парадоксов, это кажется невозможным.
Одним из самых известных парадоксов в логике является парадокс Эпимеда, который основан на противоречии между двумя простыми утверждениями. Первое утверждение гласит: «Эпимед отрицает, что все, что он говорит, правда». Второе утверждение утверждает: «Если то, что он говорит, ложно, то он говорит истину». Логическое следствие — если первое утверждение истино, то он должен говорить истину, а значит, второе утверждение также истинно. Однако, это противоречит первому утверждению. Таким образом, есть два противоречивых утверждения, которые образуют парадокс Эпимеда.
В чем же причина возникновения таких парадоксов в логике? Возможно, они являются результатом субъективного восприятия и ограниченности человеческого мышления. Логика, основанная на четких правилах и грамматике, не всегда способна учесть все нюансы и особенности философических и логических проблем. Таким образом, парадоксы показывают недостатки человеческого мышления и требуют дальнейших исследований и усовершенствований в области логики и философии.
Символика искусственного интеллекта
Искусственный интеллект (ИИ) является одной из наиболее актуальных и интересных тем современной науки. Символика, связанная с искусственным интеллектом, играет важную роль в понимании и визуализации этой новой области. Она помогает олицетворить и выразить сложные концепции и идеи, связанные с ИИ, сделав их более доступными и понятными.
Одним из ключевых символов искусственного интеллекта является «рука робота». Она символизирует идею механической силы и точности, которой обладают роботы с искусственным интеллектом. «Рука робота» также может олицетворять возможности ИИ в области автоматизации, производства и манипуляции предметами.
Еще одним символом, связанным с искусственным интеллектом, является «мозг». Визуализация мозга акцентирует внимание на интеллектуальных способностях ИИ, его способности к обучению, вычислениям и принятию решений. «Мозг» также может символизировать идею сознания и мышления, которые являются ключевыми аспектами искусственного интеллекта.
Кроме того, символика искусственного интеллекта может включать в себя такие элементы, как «цифровой код» и «алгоритмы». Эти символы указывают на важность компьютерных технологий и вычислительных процессов в развитии и функционировании искусственного интеллекта.
Искусственный интеллект — это сложная и многогранная область, и символика позволяет нам лучше понять и визуализировать ее. Она помогает создать конкретные образы и идеи, связанные с ИИ, что способствует распространению и популяризации этой важной области науки.
Парадокс Си, или доказательство неполноты Гёделя

Парадокс Си, который также называется доказательством неполноты Гёделя, является одним из наиболее известных и значимых парадоксов в логике и математике. Этот парадокс был предложен американским логиком Рэймондом Смаллианом, и он основан на противоречии в самом ядре математической логики.
Парадокс Си заключается в следующем: рассмотрим некоторую систему аксиом и правил вывода, которая называется формальной системой. В этой системе можно формулировать различные утверждения и доказывать их, используя аксиомы и правила вывода. Однако, парадокс Си показывает, что некоторые утверждения в формальной системе невозможно ни доказать, ни опровергнуть.
Суть парадокса Си заключается в том, что само утверждение «Это утверждение нельзя доказать» может быть сформулировано на языке формальной системы и является либо истинным, либо ложным утверждением. Если оно истинное, то оно не может быть доказано, иначе оно было бы ложным. Если же оно ложное, то оно может быть доказано, но тогда оно было бы истинным. Таким образом, утверждение «Это утверждение нельзя доказать» приводит к противоречию внутри самой формальной системы.
Парадокс Си является важным примером неполноты формальных систем и главным открытием Курта Гёделя в области математической логики. Он показывает, что в рамках формальной системы невозможно доказать полноту всех истинных утверждений, что оставляет пространство для неопределимости и недостижимости полной математической истины. Этот парадокс имеет большое значение как фундаментальный результат в теории формальных систем и оказывает влияние на различные области философии, логики и математики.
Парадокс лжи
Парадокс лжи является одним из самых известных и парадоксальных философских противоречий. Он основан на утверждении о лжи самого себя. Парадокс возникает, когда мы рассматриваем высказывание, которое говорит о самом себе, и запутываемся в его истинности или ложности.
Классический пример парадокса лжи звучит следующим образом: «Это предложение ложно». Допустим, если данное утверждение верно, то получается, что оно говорит правду о себе, что противоречит его собственному содержанию. С другой стороны, если предложение ложно, то оно снова говорит правду о себе, что также противоречит его собственному содержанию. Таким образом, данное высказывание оказывается как истинным, так и ложным одновременно.
Парадокс лжи является ярким примером того, как непоследовательность и противоречия могут возникать в логике. Он показывает, что некоторые высказывания могут быть одновременно истинными и ложными, что противоречит обычным правилам логики. Парадокс лжи вызывает множество философских дебатов и до сих пор не имеет однозначного решения.
Изучение парадокса лжи позволяет нам лучше понять границы и ограничения логического мышления. Он продолжает вызывать интерес и провоцировать умы ученых и философов, стимулируя дальнейшие исследования в области парадоксов и основ логики.
Антиномии Рассела

Антиномии Рассела – это классические парадоксы в логике, которые были предложены Бертраном Расселом в начале 20-го века. Они относятся к проблеме самоопределения и саморефлексии в логике.
В основе антиномий Рассела лежит парадокс самоприменения. Этот парадокс состоит в следующем: пусть А – утверждение о самом себе. Если А истинно, то оно ложно и наоборот. Таким образом, возникает противоречие, которое называется «противоречием Барбера».
Еще одной антиномией Рассела является парадокс самовключения. Он основан на утверждении, что существует множество, которое содержит в себе все множества. Если множество содержит в себе все множества, то оно содержит и само себя, что приводит к противоречию.
Антиномии Рассела поднимают важный вопрос о природе логики и возможностях ее применения. Они показывают, что логическая система может быть противоречивой и содержать самопротиворечивые утверждения. В связи с этим возникает вопрос о том, какие ограничения следует накладывать на логику и какие парадоксы могут возникать при ее применении.
Какая логика может быть истинной?
В области логики существует несколько различных систем и подходов, каждая из которых преследует свои цели и принципы. Однако, когда говорят о «истинной логике», обычно имеют в виду логическую систему, которая предоставляет надежные и последовательные методы рассуждения.
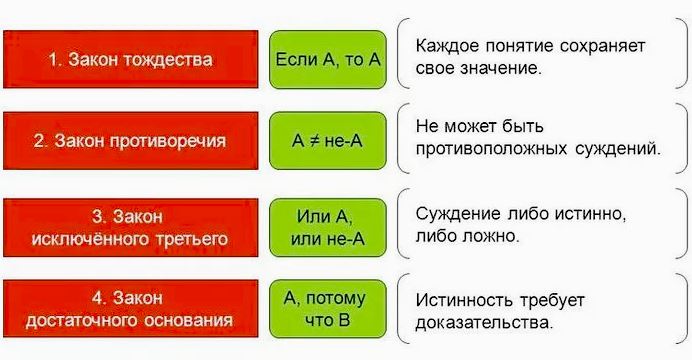
В традиционной логике, такой как классическая логика или логика первого порядка, основные понятия такие как истинность, ложность и законы логики определяются строго и однозначно. В рамках этой логики можно строить надежные и структурированные аргументы, основываясь на логических законах, таких как закон исключенного третьего и закон двойного отрицания.
Однако, существуют альтернативные системы, например, интуиционистская логика или многозначная логика. Интуиционистская логика отличается от классической логики тем, что она отрицает некоторые из основных законов классической логики, в основном в связи с использованием отрицания (например, отрицание закона исключенного третьего). Многозначная логика, с другой стороны, позволяет существование более чем двух значений истинности (например, истина, ложь и неопределенность).
Таким образом, вопрос о том, какая логика может быть истинной, связан с выбором конкретной логической системы исходя из целей и задач, которые перед ней стоят. Некоторые ситуации могут требовать строгости и надежности, которые обеспечивает классическая логика, в то время как другие ситуации могут потребовать более гибкого подхода, который предлагает альтернативная логика. В конечном счете, истинность логики определяется ее пригодностью для конкретных задач и возможностью давать надежные и последовательные рассуждения.
Суждение на основе прошлого

Суждение на основе прошлого — это процесс формирования выводов и предположений на основе прошлого опыта и знаний. Человек, основываясь на своих предыдущих наблюдениях и событиях, приходит к определенным суждениям или выводам о том, что может произойти в будущем или в определенных ситуациях.
Суждение на основе прошлого может быть полезным инструментом для принятия решений и предсказаний. Например, если человек уже несколько раз видел, что после дождя дорога становится скользкой, он может сделать вывод, что после следующего дождя тоже будет скользко и, соответственно, принять меры для безопасного передвижения.
Однако, суждение на основе прошлого также может быть неправильным или ошибочным. Оно основано на предположении, что будущие события будут повторять прошлые. Но мир постоянно меняется, и то, что произошло в прошлом, не всегда является точным предсказанием для будущего.
Также важно отметить, что суждение на основе прошлого может оказать негативное влияние на принятие новых решений и открытие для новых возможностей. Если человек всегда придерживается только прошлых опытов и не осмеливается выйти за пределы привычного, он может ограничить свой рост и развитие.
Таким образом, суждение на основе прошлого имеет свои преимущества и ограничения. Оно помогает нам сделать выводы и предсказания, но может быть неправильным в некоторых случаях. Важно уметь анализировать и учитывать как прошлый опыт, так и новые возможности, чтобы принимать более осознанные решения и двигаться вперед.
Классическая логика и причинно-следственные связи
Классическая логика является одной из основных дисциплин философии и изучает формальные законы рассуждений и выводов. Одним из важных аспектов логики является анализ причинно-следственных связей. Происхождение этого раздела связано с попыткой объяснить возникновение событий и феноменов, определить их причины и последствия.
Причинно-следственная связь предполагает, что событие или феномен, называемый следствием, имеет своей причиной другое событие или феномен. Такая связь основана на наших наблюдениях и опыте и позволяет нам предсказывать и объяснять мир вокруг нас. В классической логике причинным фактором обычно считается тот элемент, который предшествует другому и приводит к его появлению.
Однако классическая логика не всегда способна полностью объяснить и анализировать причинно-следственные связи. Она ограничена своими формальными законами и не всегда учитывает сложность реального мира. Здесь на помощь приходит диалектическая логика, которая позволяет учитывать множество факторов и противоречий, которые могут оказывать влияние на причинно-следственные связи.
Таким образом, классическая логика и причинно-следственные связи тесно связаны между собой. Логический анализ причинно-следственных связей позволяет нам лучше понять мир вокруг нас, но при этом важно учитывать его ограничения и использовать дополнительные инструменты, такие как диалектика, для полного и точного понимания сложных причинно-следственных связей.
Есть ли противоречия в причинно-следственных связях?

Противоречия в причинно-следственных связях являются предметом дискуссий в области философии и науки. В рамках классической логики причина и следствие рассматриваются как два независимых источника информации, связанных между собой. Однако, существуют случаи, когда эта связь может быть нарушена или показаться противоречивой.
Противоречия в причинно-следственных связях могут возникать из-за неполной информации или неправильного анализа. Например, если мы наблюдаем два события, следующие друг за другом, это не означает, что одно событие является причиной другого. Между ними может быть скрытый фактор, который мы не учли или не заметили.
Кроме того, причинно-следственные связи могут быть неоднозначными и зависеть от контекста. Например, если мы видим, что вода кипит при определенной температуре, мы можем сказать, что повышение температуры является причиной кипения. Однако, если добавить соль в воду, температура кипения изменится, и причинно-следственная связь станет более сложной.
В некоторых случаях противоречия в причинно-следственных связях могут указывать на неоднозначность самих понятий «причина» и «следствие». Например, если мы говорим, что стресс является причиной заболевания, это может быть истина, но также и ложь. Стресс может быть фактором, который предрасполагает к заболеванию, но не является единственной причиной.








