Секрет: как соединить 9 точек всего 4 линиями

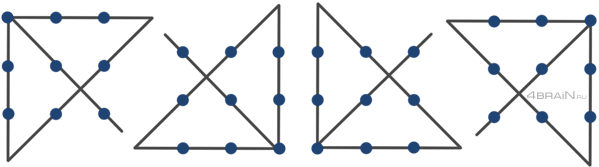
Возможно, многие из нас в детстве играли в головоломку, которая называлась «Соедини точки». Цель игры была в том, чтобы соединить 9 точек, расположенных на плоскости, всего 4 линиями, не отрывая карандаша от бумаги. Для многих эта головоломка была пугающей и неразрешимой, но на самом деле, это задание можно успешно выполнить.

Тайна заключается в том, что чтобы соединить все одним ходом, нужно встать над проблемой по-новому и выйти за рамки привычного мышления. Вместо того, чтобы думать о линиях как о прямых, нужно представить их как части эллипсов, которые образуют одну большую фигуру.

Если взглянуть внимательно на расположение точек, можно заметить, что они образуют паттерн, похожий на квадрат. Чтобы соединить все точки, нужно продлить линии, проходящие через углы квадрата. Таким образом, мы получим четыре линии, которые соединят все девять точек.

Однако, чтобы найти этот путь, нужно думать абстрактно и выходить за рамки привычного подхода. Именно такой подход поможет нам решать и другие сложные задачи в повседневной жизни и бизнесе.

Поэтому, следующий раз, когда вы столкнетесь с сложной задачей, помните о головоломке с девятью точками и попробуйте найти новый подход для ее решения. Возможно, он окажется более эффективным и приведет вас к неожиданным результатам.

Секрет решения: 9 точек, 4 линии

Задача, которая заключается в соединении девяти точек всего лишь четырьмя линиями, может показаться сложной на первый взгляд. Но на самом деле существует простой секрет, который позволяет решить эту головоломку.

Секрет заключается в том, что нужно выйти за рамки представленной области с точками. Часто люди пытаются провести линии только внутри прямоугольника, но это ограничение делает задачу невыполнимой.

Для решения головоломки необходимо мыслить абстрактно и использовать дополнительные пространства. Одним из способов решения задачи является проведение линий за пределы прямоугольника. Таким образом, можно связать все девять точек всего лишь четырьмя линиями.

Важно также подходить к решению задачи с творческим мышлением и гибкостью. Не стоит ограничивать себя традиционными представлениями, а лучше искать нетрадиционные подходы к решению. Не бойтесь экспериментировать, и вам обязательно удастся соединить все девять точек всего лишь четырьмя линиями.

Как искать оптимальное решение

Когда перед нами стоит задача найти оптимальное решение, необходимо применить систематический подход и использовать логику. В данной задаче с соединением 9 точек всего 4 линиями, важно расширить свои когнитивные границы и не ограничиваться стандартными рамками мышления.

Первым шагом в поиске оптимального решения является понимание условий задачи. Задача включает в себя 9 точек, которые нужно соединить 4 линиями, не отрывая карандаш от бумаги. Важно осознать, что линии не обязаны быть прямыми и могут иметь произвольную форму.

Далее следует провести анализ и рассмотреть все возможные варианты соединения точек. Не стоит ограничиваться привычными способами соединения точек, поскольку задача именно в поиске оптимального решения. Можно пробовать соединять точки дугами, использовать дополнительные точки для создания дополнительных линий и т.д.

Важно помнить, что в поиске оптимального решения нет однозначного правила или алгоритма. Ключевое значение имеет творческий подход и умение «видеть» возможности, которые обычно остаются незамеченными. Постоянное переосмысление и экспериментирование помогут найти наиболее эффективное решение.

В заключение, поиск оптимального решения требует гибкости мышления и умения думать за пределами заданных рамок. В данной задаче с соединением 9 точек всего 4 линиями, это означает использование творческого подхода, экспериментирование с различными вариантами и постоянное открытое мышление. Не стоит ограничиваться стандартными методами и быть готовым к неожиданным решениям.

Выбор правильной стратегии

Для успешного решения головоломки, связанной с соединением 9 точек всего 4 линиями, необходимо выбрать правильную стратегию. Это полностью зависит от вашего подхода к проблеме и умения мыслить нестандартно. Подбор стратегии влияет на вашу способность найти скрытые решения и продвигаться вперед.

Одним из вариантов стратегии может быть логическое разделение пространства на части. При таком подходе, вы можете разделить головоломку на несколько меньших задач и решать их поочередно. Это позволит вам видеть проблему с разных сторон, а также концентрироваться на одной части задачи, чтобы найти скрытые решения.

Другой вариант стратегии — это использование эвристических методов. Они позволяют искать решения, основываясь на опыте и интуиции. Вы можете пробовать разные варианты и изменять свой подход, чтобы найти более эффективное решение. Это может потребовать времени и терпения, но в итоге вы сможете найти оптимальный путь соединения точек.

Для выбора правильной стратегии важно быть гибким и открытым к новым идеям. Не бойтесь экспериментировать и пробовать разные подходы к решению головоломки. Иногда самая неожиданная стратегия может оказаться наиболее эффективной. Помните, что главное — это не количество линий, которое вы используете, а то, как хорошо вы задействуете свой ум и интуицию для нахождения решения.

Применение креативности

Применение креативности в различных сферах жизни позволяет найти оригинальные и нестандартные решения. Креативность помогает нам выходить за рамки привычного и находить новые пути достижения целей.

Одна из областей, где креативность особенно важна, это мировые лидеры и предприниматели, которые сталкиваются с постоянными вызовами и необходимостью принимать сложные решения. Креативные лидеры могут предложить инновационные и неожиданные подходы к проблемам и тем самым достичь успеха.

Также, креативность играет важную роль в развитии искусства и дизайна. Художники, дизайнеры и музыканты используют свою креативность для создания уникальных и эмоциональных произведений искусства. Они могут переосмыслить традиционные техники, экспериментировать с материалами и искать новые способы выражения своего творчества.

Креативность также может быть полезной в решении повседневных задач. Например, при планировании событий и организации встреч можно применить креативные подходы к декору, меню и развлечениям, чтобы создать незабываемые впечатления для гостей.

В целом, применение креативности позволяет нам выйти за рамки привычного и находить новые, оригинальные решения. Это способствует развитию инноваций, искусства и организации нашей повседневной жизни, делая ее более интересной и разнообразной.

Изучение задачи

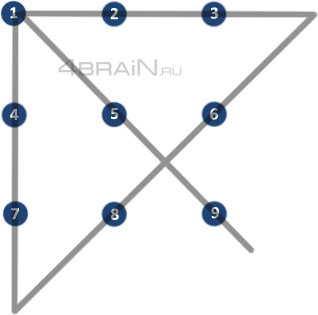
Задача о соединении 9 точек всего 4 линиями является известной головоломкой, которая представляет интерес для широкого круга людей. В этой задаче необходимо соединить все 9 точек, расположенных в сетке 3×3, с помощью четырех линий без отрыва карандаша от бумаги и без повторного прохода по одной и той же линии.

Изначально может показаться, что такую задачу невозможно решить. Однако, существует несколько подходов и стратегий, которые позволяют найти решение. Один из таких подходов — взять задачу нестандартно, выйти за пределы сетки и визуализировать варианты, которые не являются ограничениями задачи.

Для решения этой задачи можно использовать различные комбинации прямых линий, дуги и изгибы. Важно помнить, что в данной задаче нам необходимо соединить все точки, а не просто провести линии между некоторыми парами точек.

Ознакомившись с различными подходами и стратегиями, можно перейти к решению задачи. Необходимо приступить к поиску наилучшего варианта сочетания линий, который удовлетворит всем условиям задачи и соединит все 9 точек с помощью четырех линий. При этом важно сохранять гибкость в мышлении и быть готовым к неожиданным решениям.

Визуализация проблемы

Задача заключается в том, чтобы соединить девять точек, расположенных в виде 3х3 таблицы, с помощью всего лишь четырех линий.

На первый взгляд может показаться, что это задание не слишком сложное, ведь нарисовать четыре линии, соединяющие девять точек, кажется не таким уж непосильным. Однако, на самом деле, решение этой задачи требует остроумия и творческого подхода.

Если попытаться соединить точки, следуя обычным правилам соединения линиями от одной точки к другой, то очевидно, что мы получим пять линий, а не четыре. Вот в чем кроется сложность задачи.

При визуализации проблемы становится понятно, что необходимо найти более нетривиальное решение, которое позволит соединить все точки только четырьмя линиями без отрыва карандаша от бумаги.

Анализ возможных вариантов

В условии задачи о том, как соединить 9 точек всего 4 линиями, необходимо провести анализ возможных вариантов решения.

1. Первый вариант – все линии идут по вертикали и горизонтали. В этом случае каждая линия будет проходить через 3 точки, итого мы получим 3 линии, что меньше, чем нужно.

2. Второй вариант – использование диагональных линий. В этом случае каждая линия будет проходить через 4 точки, итого мы получим 4 линии. Однако, при таком подходе остается одна неразрешенная точка, которая недоступна для связи.

3. Третий вариант – использование комбинации линий по вертикали, горизонтали и диагонали. В этом случае можем сократить количество линий до 4, соединяя по 2 точки диагональной линией, а остальные точки – вертикальными и горизонтальными линиями.

4. Четвертый вариант – использование овальной линии. В этом случае можем провести линию, которая проходит через все 9 точек, одновременно соединяя каждую из них.

Таким образом, проведя анализ возможных вариантов, мы можем прийти к выводу, что наилучшим решением будет третий вариант — использование различных линий и комбинация их между собой.

Рассмотрение ограничений

Чтобы решить задачу о соединении 9 точек всего 4 линиями, необходимо учесть некоторые ограничения. Во-первых, линии должны быть рисованы без отрыва карандаша от бумаги. Это означает, что одна линия не может быть прервана и продолжена в другом месте.

Во-вторых, нужно использовать только 4 линии, что означает, что не разрешается проводить больше или меньше линий. Количество линий должно быть строго равно 4.

Третье ограничение заключается в том, что линии должны быть прямыми. Иными словами, они не могут иметь изгибов или поворотов.

Четвертое ограничение состоит в том, что линии должны пройти через все 9 точек, а не только некоторые из них. Это означает, что ни одна точка не может быть оставлена без соединения.

Учитывая все эти ограничения, решение задачи требует творческого и нетрадиционного подхода. Необходимо искать необычные способы проведения линий, чтобы все они соединили все 9 точек, при соблюдении ограничений задачи.

Поиск оптимального решения

Решение головоломки, связанной соединением 9 точек всего 4 линиями, требует тщательного поиска оптимального варианта. Для этого необходимо проанализировать все возможные варианты соединения точек и найти наиболее эффективное решение.

При поиске оптимального решения необходимо учитывать, что линии должны проходить через все 9 точек, не отрываясь от них. Также важно найти наименьшее количество линий, чтобы решение было компактным и эффективным.

Для начала поиска оптимального решения можно использовать метод перебора. Попробовать соединить точки различными способами и оценить результат. Однако, такой подход может быть долгим и неэффективным из-за большого количества вариантов.

Более эффективным подходом может быть использование математических и логических методов. Например, можно построить таблицу возможных соединений и применить методы оптимизации для выбора наиболее эффективного решения. Также можно использовать алгоритмы поиска, такие как алгоритмы графов, чтобы найти наименьшее количество линий для соединения всех точек.

Поиск оптимального решения требует внимательности, тщательного анализа и применения различных методов. В конечном итоге, правильное решение должно удовлетворять всем условиям задачи и быть наименее затратным в применении линий.

Разбиение задачи на подзадачи

Разбиение задачи на подзадачи представляет собой методологию, которая помогает разложить сложную задачу на более простые и управляемые единицы. Это позволяет более эффективно решать сложные проблемы, предпринимать последовательные шаги и улучшать продуктивность.

Одним из основных преимуществ такого подхода является возможность более глубокого понимания и анализа задачи. Разбиение на подзадачи помогает исследовать каждый аспект сложной проблемы отдельно, раскрывая детали и особенности. Это позволяет выявить возможные проблемы и пути их решения.

Другим важным аспектом разбиения задачи на подзадачи является возможность параллельной работы. Каждая подзадача может быть решена независимо от других, что позволяет эффективно использовать ресурсы и распределить задачи между участниками команды. Это увеличивает скорость выполнения задач и позволяет достигать лучших результатов.

Для разбиения задачи на подзадачи можно использовать различные методики, такие как декомпозиция, структурный анализ, а также составление диаграмм и схем. Разбиение может происходить по различным параметрам, например, по функциональности, приоритетности или временным ограничениям.

Важно помнить, что разбиение задачи на подзадачи должно быть логичным и последовательным. Каждая подзадача должна быть четко определена и иметь назначенный ответственный. Также необходимо учесть зависимости между подзадачами и разработать план работы, который позволит эффективно управлять процессом выполнения задачи.

Построение матрицы решений

Для решения головоломки, связанной с соединением 9 точек всего 4 линиями, необходимо использовать метод построения матрицы решений. Идея заключается в том, чтобы создать таблицу, в которой будут представлены все возможные комбинации линий, связывающих точки.

Для начала, пронумеруем точки от 1 до 9 для удобства. Затем создадим таблицу с 9 строками и 4 столбцами. В каждой ячейке таблицы будем указывать, какая линия соединяет две точки.

В первом столбце таблицы будем обозначать точку, из которой выходит линия, а во втором столбце — точку, в которую она входит. В третьем и четвертом столбцах таблицы будем обозначать, соединяет ли линия две точки или проходит она мимо.

Например, в клетке таблицы на пересечении первой строки и первого столбца стоит число 1, обозначающее, что первая линия соединяет точки 1 и 2. Если в клетке стоит число 0, это означает, что линия проходит мимо соответствующих точек.

Построив такую таблицу, можно перебрать все возможные комбинации линий и выбрать ту, которая удовлетворяет условиям задачи — соединяет все 9 точек всего 4 линиями.

Применение теории графов

Теория графов является одной из важнейших разделов математики, которая находит применение во многих областях науки и техники. Ее основная задача — изучение объектов, состоящих из вершин и ребер, образующих связи между ними. Применение этой теории позволяет решать разнообразные задачи, связанные с анализом и моделированием сложных систем.

Одним из примеров применения теории графов является решение известной головоломки, связанной с соединением девяти точек всего четырьмя линиями без отрыва карандаша. Это задание особенно интересно с точки зрения теории графов, так как оно требует поиска оптимального решения, учитывая ограничения и связи между элементами.

Нахождение решения подобных головоломок основывается на принципах теории графов. Сначала строится граф с вершинами, соответствующими точкам задания, и ребрами, обозначающими возможные связи между ними. Затем осуществляется поиск оптимального пути или комбинации ребер, удовлетворяющих условиям задачи.

Теория графов получила широкое применение в алгоритмах маршрутизации, планировании транспортных сетей, проектировании социальных и электрических сетей, анализе связей в сети Интернет и многих других областях. Благодаря этой теории можно осуществлять моделирование сложных систем, оптимизировать их работу и принимать взвешенные решения на основе математических моделей.