
Статистика является неотъемлемой частью многих областей науки и бизнеса, поскольку предоставляет нам инструменты для понимания мира на основе доступных данных. Статистические методы анализа данных позволяют нам делать выводы на основе полученной информации, выявлять зависимости и тренды, прогнозировать будущие события и принимать обоснованные решения.
Одним из важных аспектов статистического анализа данных является их описательная статистика. Эта методика позволяет нам суммировать и представить информацию о наборе данных, используя такие показатели, как среднее значение, медиана, дисперсия и стандартное отклонение. Описательная статистика помогает нам понять характеристики данных и сделать первичные выводы.
Кроме описательной статистики, существуют статистические методы, которые позволяют нам делать более точные выводы на основе имеющихся данных. Данные методы включают в себя такие аспекты, как статистическая значимость, корреляционный анализ, регрессионный анализ, анализ дисперсии и другие. Они помогают нам определить, есть ли значимые различия между разными группами данных, выявлять взаимосвязи между переменными и строить модели для прогнозирования будущих значений.
Раздел 1: Основные понятия
Статистические методы анализа данных являются мощным инструментом для работы с информацией и получения полезных выводов. Они позволяют проводить обработку и интерпретацию данных на основе определенных математических и статистических методов.
Популяция — это общая группа объектов или событий, которые подлежат анализу. Например, популяция может быть составлена из всех студентов университета или всех продуктов определенной компании.
Выборка — это подмножество популяции, которое выбирается для проведения анализа. Выборка может быть случайной или нерандомизированной. Случайная выборка обеспечивает более репрезентативные результаты и позволяет делать выводы о всей популяции.
Параметры выборки — это числовые характеристики, которые описывают выборку. Они могут быть средним значением, медианой, стандартным отклонением и другими статистическими показателями.
Гипотеза — это утверждение или предположение, которое проверяется при помощи статистических методов. Гипотеза может быть нулевой (предполагает отсутствие различий или эффекта) или альтернативной (предполагает наличие различий или эффекта).
Уровень значимости — это вероятность ошибки при отклонении нулевой гипотезы, когда она является верной. Обычно используются уровни значимости 0,05 или 0,01, что означает, что вероятность совершить ошибку равна 5% или 1% соответственно.
Статистическое тестирование — это процесс проверки гипотезы на основе наблюдаемых данных и статистических методов. Результаты тестирования позволяют сделать выводы о том, является ли гипотеза верной или нет.
Доверительный интервал — это интервал, в котором, с заданной вероятностью, находится истинное значение параметра. Он позволяет оценить точность и надежность результатов статистического анализа.
Параметр и статистика
В статистике используются два основных понятия — параметр и статистика. Параметр — это числовая характеристика генеральной совокупности. Он может представлять среднее значение, дисперсию, медиану и другие характеристики распределения данных. Параметр определяется для всей генеральной совокупности и служит для описания основных характеристик данных.
Статистика, в свою очередь, является числовой характеристикой выборки, полученной из генеральной совокупности. Она предназначена для оценки параметров и проведения статистических тестов. В отличие от параметра, статистика может изменяться в зависимости от выборки, поэтому для получения достоверных результатов необходимо проводить большое количество экспериментов или анализировать большое количество данных.
Статистика может быть описательной или выводимой. Описательная статистика предназначена для описания данных и включает в себя среднее значение, дисперсию, медиану и другие характеристики. Выводимая статистика используется для проверки гипотез и определения степени значимости различий между выборками. Для этого используются такие показатели, как t-критерий Стьюдента, F-критерий фишера и другие методы.
Понимание параметров и статистики является важным для проведения анализа данных и принятия важных решений. Они позволяют получить объективные числовые характеристики данных и оценить степень достоверности полученных результатов. Без них невозможно провести серьезный и надежный анализ, который может быть использован в научных исследованиях, бизнес-аналитике и других сферах деятельности.
Распределение и выборка

Распределение – это вероятностная функция, которая описывает вероятность появления различных значений случайной величины. Распределение может быть дискретным или непрерывным. В дискретном распределении значения случайной величины могут принимать только определенные, разделенные друг от друга значений, например, количество лет в человеческой жизни. В непрерывном распределении значения случайной величины могут принимать любые значения из некоторого диапазона, например, время ожидания в очереди.
Выборка – это подмножество значений, взятых из генеральной совокупности, которая представляет собой полный набор значений случайной величины. Выборка используется для изучения и анализа данных, когда исследование всей генеральной совокупности непрактично или невозможно. Выборка должна быть представительной и случайной, чтобы полученные результаты можно было обобщить на генеральную совокупность.
Выборка может быть простой – каждый элемент выборки полностью независим и равновероятно выбран из генеральной совокупности – или сложной – элементы выборки могут зависеть друг от друга или иметь различные вероятности быть выбранными. Размер выборки – это количество элементов в выборке и может варьироваться в зависимости от цели исследования и доступных ресурсов.
Распределение выборки – это распределение значений, полученных из выборки. Распределение выборки может быть использовано для оценки параметров генеральной совокупности, поиска типичных значений или аномалий, проверки гипотез и т. д. Часто распределение выборки аппроксимируется некоторым заранее известным статистическим распределением, таким как нормальное или равномерное распределение. Рассмотрение распределения выборки позволяет сделать выводы о характеристиках генеральной совокупности и обобщить полученные результаты на все ее элементы с определенной степенью уверенности.
Раздел 2: Работа с данными
Анализ данных — это процесс сбора, организации, интерпретации и представления данных, с целью изучения паттернов, отношений и тенденций. Для успешного анализа данных необходимы навыки работы с различными статистическими методами, которые позволяют извлекать информацию из собранных данных.
Статистические методы анализа данных включают в себя множество техник, таких как описательная статистика, визуализация данных, проверка гипотез, анализ корреляции и регрессии, анализ временных рядов и др. Они позволяют исследователям извлекать информацию, делать выводы и прогнозировать на основе исследуемых данных.
Для работы с данными необходимо провести сбор и предобработку. Сбор данных включает в себя выбор источников данных, определение переменных для измерения и установление методов сбора данных. Предобработка данных включает в себя очистку данных от ошибок и выбросов, обработку пропущенных значений и преобразование данных в формат, который можно использовать для анализа.
Описательная статистика представляет собой первичный анализ данных, включающий расчет основных статистических показателей, таких как среднее, медиана, мода, дисперсия, интерквартильный размах и др. Она помогает исследователю получить представление о распределении данных и выявить основные характеристики выборки.
Для визуализации данных можно использовать различные графические методы, такие как гистограммы, диаграммы рассеивания, круговые диаграммы, ящики с усами и др. Визуализация данных помогает исследователю наглядно представить распределение данных и выявить возможные связи и паттерны.
Помимо описательной статистики и визуализации данных, статистические методы анализа также включают проверку гипотез и построение статистических моделей. На основе статистического анализа можно сделать выводы о значимости связей и различий между переменными, а также сделать прогнозы на основе имеющихся данных.
Сбор данных
Сбор данных — это первый и один из самых важных этапов в статистическом анализе данных. Для получения достоверных и репрезентативных результатов необходимо собирать данные в соответствии с определенными методами и правилами.
Сбор данных может осуществляться различными способами, включая анкетирование, наблюдение, проведение экспериментов или использование вторичных источников данных. Один из самых популярных методов сбора данных — опрос, который позволяет получить информацию от различных групп и категорий людей.
При сборе данных необходимо определить цель исследования, выбрать участников, разработать опросник или набор вопросов, выбрать способ представления данных (например, в виде числовых значений или категорий), а также провести анализ данных.
Важным аспектом сбора данных является сохранение их конфиденциальности. Респондентам должно быть обеспечено анонимный уровень конфиденциальности, чтобы они могли отвечать на вопросы откровенно и без страха перед негативными последствиями.
Сбор данных также может включать проверку наличия ошибок или недостоверных данных. Для этого используются различные методы и инструменты, такие как статистический анализ выбросов и проверка на логические ошибки.
В целом, сбор данных — важный этап в процессе анализа данных, который помогает получить информацию о целевой группе или явлении. Правильно собранные и обработанные данные позволяют сделать качественные выводы и принять обоснованные решения.
Предобработка данных
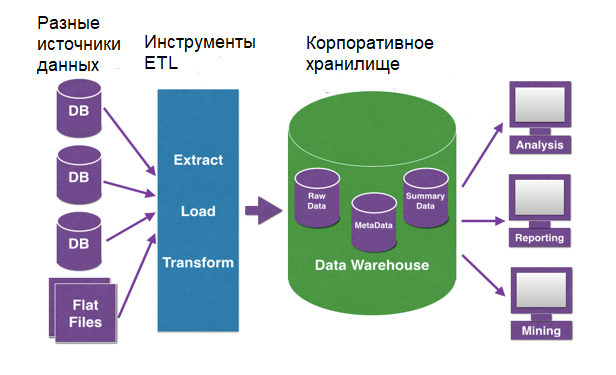
Предобработка данных – это важный этап в анализе и обработке больших объемов информации. Она включает в себя различные операции по очистке и преобразованию данных для дальнейшего анализа и интерпретации. Без предварительной обработки данных невозможно получить достоверные и точные результаты исследования.
Одной из основных задач предобработки данных является удаление или исправление ошибок и пропусков. Нерепрезентативные данные могут исказить итоговые результаты, поэтому необходимо проанализировать общую структуру данных и выявить аномалии. Также важно преобразовать данные в форматы, пригодные для анализа. Это может включать преобразование данных в числовые значения, удаление ненужных символов или изменение формата даты и времени.
Кроме того, важно установить соответствие данных определенным стандартам. Например, при анализе текстовых данных можно провести лемматизацию или стемминг для унификации словоформ. Также можно провести нормализацию данных, например, привести все значения к одному диапазону или единице измерения.
Предобработка данных также может включать агрегацию и группировку данных. Возможно, необходимо объединить несколько таблиц или данных и провести агрегацию по определенным параметрам. В этом случае можно использовать функции сводных таблиц или группировку данных по ключевым полям.
Объем и сложность предобработки данных зависит от их источника и цели исследования. Однако важно помнить, что качественная предобработка данных является основой для дальнейшего анализа и получения надежных результатов.
Раздел 3: Основные методы анализа
В разделе 3 рассматриваются основные методы анализа данных, которые широко применяются в статистической науке и позволяют проводить качественные и количественные исследования. Одним из основных методов является дескриптивный анализ данных. Этот метод позволяет описать основные характеристики данных, такие как среднее значение, медиана, размах, дисперсия и другие.
Другим важным методом анализа данных является корреляционный анализ. Он позволяет определить, существует ли связь между двумя или более переменными. Корреляционный анализ позволяет оценить силу и направление связи, а также провести статистическую проверку ее значимости.
В разделе также рассматривается регрессионный анализ, который позволяет предсказывать значения одной переменной на основе значений других переменных. Регрессионный анализ позволяет оценить влияние различных факторов на исследуемую переменную и построить модель, которая будет наилучшим образом описывать зависимость между переменными.
Один из основных методов анализа данных, рассматриваемых в данном разделе, — это анализ дисперсии. Анализ дисперсии позволяет определить, есть ли статистически значимые различия между средними значениями групп или образцов. Этот метод широко используется в исследованиях медицины, образования, экономики и других областях.
В заключение раздела 3 рассматривается метод структурного моделирования. Этот метод позволяет исследовать сложные взаимосвязи между переменными и построить модель, которая будет описывать эти взаимосвязи. Структурное моделирование позволяет определить, как различные факторы влияют на конечные результаты и предсказывать будущие события.
Описательная статистика
Описательная статистика – это раздел статистики, который позволяет описать и анализировать основные характеристики данных без проведения формальной статистической инференции. Она служит основой для дальнейшего анализа данных и позволяет получить представление о распределении, центральной тенденции, вариации и других важных свойствах выборки или популяции.
Для анализа данных в описательной статистике применяются различные методы и показатели. Важнейшими из них являются меры центральной тенденции, которые представляют собой значения, отображающие типичные или средние значения в выборке или популяции. Такие меры включают среднее арифметическое, медиану и моду. С помощью мер центральной тенденции можно определить, какое значение является наиболее вероятным или наиболее типичным в выборке.
Описательная статистика также позволяет изучать вариацию данных. Вариация представляет собой различие или разброс значений в выборке или популяции. Ее можно измерить с помощью таких показателей, как дисперсия, стандартное отклонение и коэффициент вариации. Чем больше вариация, тем больше различие между значениями в выборке.
Для представления результатов описательной статистики удобно использовать графики и таблицы. Например, гистограмма может визуально показать распределение данных, а диаграмма размаха — разброс значений. Таблицы позволяют сравнивать различные характеристики выборки или популяции и сделать выводы о взаимосвязи между ними.
Статистические тесты
Статистические тесты являются основным инструментом анализа данных в статистике. Они позволяют проверить гипотезы и делать выводы на основе имеющихся данных. Статистические тесты могут быть применены для анализа различных типов данных, таких как числовые данные, категориальные данные, временные ряды и др.
Один из наиболее распространенных статистических тестов — t-тест, который используется для сравнения средних значений двух групп. Т-тест позволяет проверить гипотезу о том, что средние значения двух групп статистически значимо различаются или нет. Этот тест может быть применен в различных областях, например, для сравнения эффективности лекарственных препаратов или оценки влияния рекламных кампаний на продажи.
Другой широко используемый статистический тест — анализ дисперсии (ANOVA), который применяется для сравнения средних значений более чем двух групп. ANOVA позволяет определить, есть ли статистически значимые различия между средними значениями разных групп. Например, этот тест может быть использован для сравнения средних значений доходов в разных регионах страны или для оценки влияния разных факторов на производительность работников в компании.
Кроме того, существует множество других статистических тестов, которые могут быть применены для решения конкретных задач. Например, тест на независимость хи-квадрат используется для проверки наличия связи между двумя категориальными переменными, корреляционный анализ используется для оценки силы и направления связи между двумя или более непрерывными переменными, и т.д.
Важно правильно выбрать и применить статистический тест, исходя из постановки задачи и особенностей имеющихся данных. Также следует учитывать предпосылки теста, чтобы полученные результаты были надежными и интерпретируемыми. Использование статистических тестов позволяет сделать более обоснованные выводы на основе имеющихся данных и принять меры на основе этих выводов.








