Схема умозаключения по логическому квадрату: основные принципы и использование

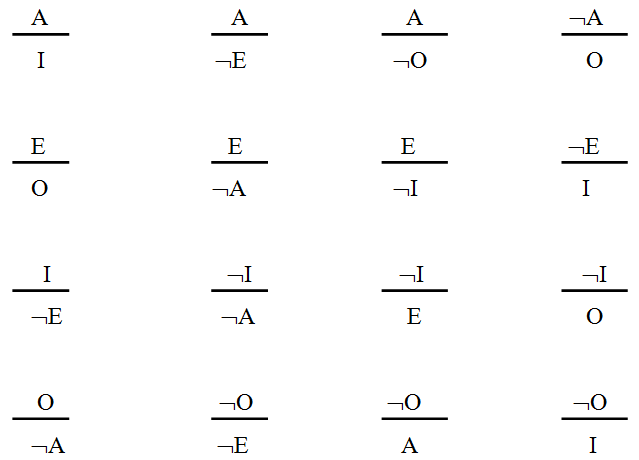
Логическое мышление – это способность человека логически рассуждать и делать выводы на основе фактов и предположений. Одним из методов логического мышления является использование схемы умозаключения по логическому квадрату.

Логическое квадрат – это графическое представление логических операций и связей между ними. Оно состоит из четырех ячеек, каждая из которых представляет одно из логических утверждений: а, не а, b, не b. В зависимости от значений этих утверждений можно сделать различные логические выводы.

Схема умозаключения по логическому квадрату позволяет делать выводы на основе заданных утверждений. Она позволяет определить связи между различными утверждениями и вывести на основе этих связей правильные логические заключения. Используется эта схема в различных областях знаний, таких как математика, философия, информатика и др.

Главное преимущество схемы умозаключения по логическому квадрату состоит в том, что она позволяет систематизировать и упорядочить информацию, а также делать точные и надежные выводы. Кроме того, она помогает развивать логическое мышление и улучшать аналитические навыки.

В заключение, схема умозаключения по логическому квадрату является мощным инструментом для логического анализа и рассуждений. Она помогает выявить связи между утверждениями и сделать правильные выводы на основе этих связей. Правильное использование данной схемы позволяет структурировать информацию и принимать обоснованные решения в различных областях деятельности человека.

Схема умозаключения по логическому квадрату

Схема умозаключения по логическому квадрату представляет собой инструмент для анализа и оценки рассуждений и умозаключений. Основными принципами этой схемы являются логическая связь между причиной и следствием, логическая связь между общим и частным, логическая связь между сходством и различием. Эти принципы позволяют структурировать информацию и делать выводы на основе логических принципов.

Схема умозаключения по логическому квадрату состоит из четырех частей, каждая из которых отражает конкретный аспект анализа. В первой части схемы рассматривается причинно-следственная связь. Здесь необходимо определить, какая информация может служить причиной, а какая — следствием. Вторая часть схемы посвящена общему и частному. В этой части необходимо выявить общие идеи и понятия, а также их отношение к конкретным примерам или особенностям. Третья часть схемы касается сходства и различия. Здесь нужно выделить общие и отличительные черты и сравнить их между собой. И, наконец, четвертая часть схемы посвящена выводу и оценке. В этой части делается заключение на основе проведенного анализа и выносится оценка.

Схема умозаключения по логическому квадрату является универсальным инструментом для анализа и оценки умозаключений. Она может быть использована в различных сферах, таких как философия, наука, логика, аргументация и т.д. С помощью этой схемы можно разобраться в сложной информации, выделить ключевые аспекты и сделать логически обоснованные выводы. Кроме того, схема умозаключения по логическому квадрату помогает развивать критическое мышление и аргументацию, что важно при принятии решений и анализе информации.

Основные принципы логического квадрата

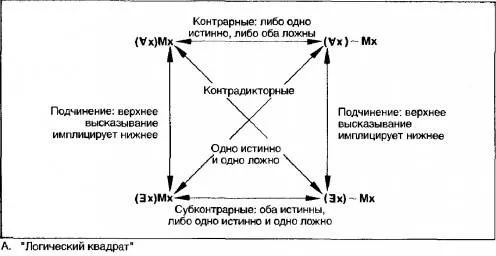
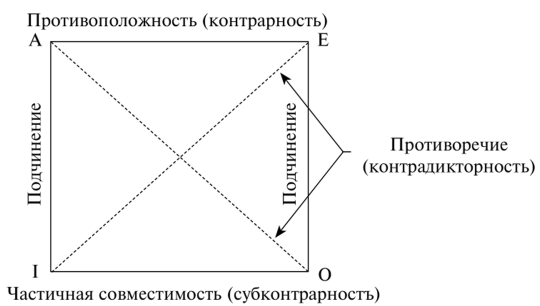
Логический квадрат — это важный инструмент логики, который позволяет систематически и логично рассуждать об отношениях между утверждениями. Он основан на четырех основных принципах, которые образуют его структуру и определяют его функциональность.

Первый принцип логического квадрата — принцип противоречия. Согласно этому принципу, два утверждения не могут быть одновременно истинными и ложными одновременно. Если одно утверждение истинно, то другое должно быть ложным, и наоборот. Этот принцип позволяет определить логическую противоположность истинного утверждения.

Второй принцип — принцип исключенного третьего. Согласно этому принципу, каждое утверждение может быть либо истинным, либо ложным, без каких-либо других вариантов. Это означает, что нет третьего пути или третьего состояния для утверждения.

Третий принцип — принцип идентичности. Согласно этому принципу, утверждение всегда идентично самому себе. То есть, если что-то утверждается, то это остается верным независимо от других факторов. Этот принцип позволяет нам делать выводы на основе информации, которая уже известна.

Четвертый принцип — принцип противоположности. Согласно этому принципу, для каждого утверждения существует противоположное утверждение. Если одно утверждение истинно, то его противоположное ложно, и наоборот. Этот принцип позволяет нам определять логическое противоположное утверждению.

Точность и строгость

В логике точность и строгость являются важными принципами, которые позволяют достичь надежных и верных выводов. Используя схему умозаключения по логическому квадрату, мы можем гарантировать, что наши выводы основаны на точных и строгих предпосылках.

Один из способов достичь точности и строгости в логическом рассуждении — это ясное формулирование предпосылок и выводов. Предпосылки должны быть ясными и однозначными, чтобы их можно было легко проверить и использовать для получения выводов. Выводы должны быть прямыми и определенными, не допускающими различных толкований.

Еще одним важным принципом точности и строгости является отсутствие противоречий в рассуждениях. Все предпосылки должны быть согласованы и не должны противоречить друг другу. Это позволяет избежать некорректных выводов и создает уверенность в достоверности рассуждений.

Используя таблицу истинности, мы можем проверить точность и строгость наших логических умозаключений. Таблица истинности показывает все возможные комбинации истинности для всех предпосылок и выводов. Если все комбинации согласуются с правилами логического квадрата, то наше умозаключение точно и строго.

Систематичность и последовательность

Логическое мышление и умозаключение базируются на систематичности и последовательности. Они являются основными принципами логического квадрата и представляют собой неотъемлемые составляющие рационального мышления.

Систематичность предполагает организацию информации и аргументов в логический порядок. Это означает, что все факты, доводы и выводы должны быть расположены таким образом, чтобы создавать структуру и логическую связь между ними. Систематичность помогает увидеть полную картину и избежать противоречий и непоследовательностей в рассуждениях.

Последовательность в логическом мышлении подразумевает логичное следование одного утверждения или аргумента за другим. Это означает, что каждое утверждение или аргумент должно быть связано с предыдущим и следующим, создавая цепочку логического рассуждения. Последовательность позволяет лучше понять структуру аргументации и увидеть логическую последовательность рассуждений.

Систематичность и последовательность являются важными инструментами логического мышления и помогают избегать ошибок в рассуждениях. Они позволяют адекватно анализировать и оценивать информацию, строить логичные аргументы и делать выводы на основе имеющихся фактов. Важно развивать навыки систематичности и последовательности для достижения более высокой степени логической точности и аргументации.

Применение схемы умозаключения

Схема умозаключения, основанная на логическом квадрате, полезна во многих областях, где требуется анализ и оценка информации. Она может быть использована в научных исследованиях, философском анализе, правовой и логической аргументации, а также в повседневной жизни для принятия рациональных решений.

Основные принципы схемы умозаключения помогают структурировать информацию и определить логическую связь между утверждениями. Это позволяет провести анализ аргументов и проверить их достоверность и обоснованность. Схема умозаключения помогает отделить факты от предположений, выделить причинно-следственные связи и оценить вероятность различных сценариев.

При использовании схемы умозаключения важно учитывать контекст и представленные данные. Необходимо быть внимательным и осторожным, чтобы избежать ошибок и ложных заключений. Критическое мышление и аналитические навыки помогут оценить достоверность и степень уверенности в полученных результатах.

Схема умозаключения также может быть полезна при принятии решений. Она помогает оценить различные варианты и выбрать наиболее оптимальный. Анализируя факты и доводы, можно прийти к логическому выводу и принять обоснованное решение. Это особенно важно в сложных ситуациях, когда нужно учесть множество факторов и возможных последствий.

Итак, схема умозаключения на основе логического квадрата имеет широкий спектр применения. Она помогает структурировать информацию, оценивать достоверность аргументов и принимать обоснованные решения. Важно развивать навыки логического мышления и критического анализа для эффективного использования данной схемы.

Научные исследования

Научные исследования играют ключевую роль в развитии науки и знания. Они являются основой для получения новых открытий, углубления понимания окружающего мира и нахождения ответов на важные вопросы. Научные исследования базируются на систематическом исследовании фактов, проведении экспериментов, анализе данных и применении логического мышления.

В процессе научных исследований ученые формулируют исходные гипотезы, разрабатывают методики исследования, собирают и анализируют данные, а затем делают выводы на основе полученных результатов. Важным принципом научных исследований является проверка гипотез, то есть установление, верна ли предполагаемая связь между явлениями или является ли результат статистически значимым.

Научные исследования проводятся в различных областях знания, таких как физика, химия, биология, психология, экономика и многие другие. Они помогают расширить наши знания о природе мира, совершенствовать технологии, разрабатывать новые лекарства и решать актуальные проблемы общества.

Научные исследования часто ведутся с применением современных технологий и методов, таких как компьютерное моделирование, генетическая инженерия, искусственный интеллект и другие. Они позволяют получить более точные и надежные результаты, а также сократить время и затраты на проведение исследований.

Важным аспектом научных исследований является их общественное значение. Они способствуют развитию образования, формированию инновационной экономики, улучшению качества жизни людей и решению глобальных проблем, таких как изменение климата, энергетическая безопасность и другие.

Решение повседневных задач

В повседневной жизни регулярно возникают различные задачи, которые требуют логического подхода для их решения. Используя схему умозаключения по логическому квадрату, можно систематизировать свои мысли и грамотно аргументировать свои выводы.

Прежде всего, необходимо правильно определить проблему и поставить перед собой задачу. Затем, следует анализировать все имеющиеся факты и данные, используя логические операции:

• Конъюнкция — сочетание двух или более условий, которые должны быть выполнены одновременно;
• Дизъюнкция — выбор одного из нескольких взаимоисключающих условий;
• Импликация — связь между причиной и следствием;
• Инверсия — замена истинности условия на ложность и наоборот.

После анализа фактов, необходимо сформулировать логическое утверждение и провести рассуждения на его основе. Важно помнить, что утверждение должно быть корректным и достаточно обоснованным.

В процессе решения повседневных задач, логическое мышление помогает структурировать информацию, проводить анализ ситуации, принимать обоснованные решения и избегать логических ошибок. Таким образом, схема умозаключения по логическому квадрату является незаменимым инструментом в повседневной жизни, помогающим преодолевать трудности и решать задачи эффективно и логично.

Преимущества использования схемы

Схема умозаключения по логическому квадрату предоставляет ряд преимуществ, которые делают ее полезным инструментом для анализа и организации логических предпосылок и выводов.

Визуальная наглядность: Схема представляет сложные логические конструкции в простой и понятный форме, что облегчает восприятие информации и позволяет быстрее определить логическую целостность аргументов.

Структурированность: Схема имеет четкую структуру, где каждый элемент занимает определенное место. Это позволяет легко распознать связи между предпосылками и выводами, а также идентифицировать логические ошибки в рассуждениях.

Упрощение комплексных аргументов: Схема упрощает сложные аргументы, разбивая их на отдельные составные части. Это позволяет лучше понять причинно-следственные связи и логические отношения между элементами.

Четкость границ: Схема позволяет ясно определить, какие элементы относятся к предпосылкам, а какие — к выводам. Это помогает логически анализировать информацию и делать точные выводы на основе имеющихся данных.

Удобство использования: Схема является удобным и действенным инструментом для работы с логическими рассуждениями. Она позволяет систематизировать информацию, выявить логические ошибки и сделать выводы на основе анализа предпосылок.

В целом, схема умозаключения по логическому квадрату предоставляет надежный и эффективный метод для анализа логических аргументов. Ее использование помогает более полно и точно понять предпосылки и выводы, а также выявить возможные ошибки в логике представленных аргументов.

Увеличение эффективности мышления

Развитие мышления является одним из ключевых аспектов успешности в различных сферах жизни. Оно позволяет анализировать информацию, принимать взвешенные решения и быстро реагировать на изменения.

Одним из способов увеличения эффективности мышления является развитие логического мышления. Логическое мышление позволяет структурировать информацию, проводить анализ, выявлять причинно-следственные связи и прогнозировать результаты.

Для развития логического мышления можно использовать схему умозаключения по логическому квадрату. Она позволяет систематизировать информацию, выявить противоречия, установить общие закономерности и сделать выводы.

Кроме того, для увеличения эффективности мышления полезно тренировать свою память. Память позволяет сохранять и восстанавливать информацию, что является основой для анализа и принятия решений. Существуют различные упражнения, которые помогают развить память, такие как решение головоломок, запоминание числовых последовательностей и использование ассоциативных карт.

Повышение точности выводов

Для повышения точности выводов в логическом квадрате следует придерживаться нескольких принципов.

Во-первых, необходимо соблюдать принцип непротиворечивости. Это означает, что внутри каждого квадрата логического квадрата не должно быть противоречий. Например, если в качестве предпосылки дано, что «Все птицы летают», то вывод «Это птица, следовательно она летает» будет точным.

Во-вторых, в логическом квадрате следует придерживаться принципа достаточности. Это означает, что для сделанного вывода должны быть представлены все необходимые предпосылки. Например, если сделан вывод «Этот объект двигается, следовательно он живой», то необходимо представить все предпосылки, на основании которых этот вывод был сделан.

В-третьих, важно следить за принципом нетривиальности. Это означает, что выводы должны быть не тривиальными и содержать новую информацию, которая не является простым повторением предпосылок. Например, если предпосылка гласит «Все коты мяукают» и вывод гласит «Это мяукающее существо — кот», то этот вывод является нетривиальным, так как содержит информацию, не указанную явно в предпосылке.

Соблюдение данных принципов позволит повысить точность выводов в логическом квадрате и сделать их более осмысленными и значимыми.