Задания по математике для 5 класса играют важную роль в формировании базовых навыков учеников. Сегодня мы рассмотрим несколько интересных задач, которые помогут развить логическое мышление и математическую интуицию у ребенка.
Задача 1.
Мама и папа купили 3 рулона ткани каждый длиной по 2 метра 75 сантиметров. Сколько метров ткани было куплено всего?
Для решения этой задачи необходимо сложить длины всех рулонов. Сначала переведем сантиметры в метры, поделив на 100. Затем сложим все длины и получим общую длину ткани.
Задача 2.
Поле для игры в футбол имеет форму прямоугольника. Длина поля 80 метров, ширина — в 3 раза меньше. Какая площадь поля?
Чтобы найти площадь прямоугольника, необходимо умножить длину на ширину. Длина поля уже известна, остается найти ширину. Зная, что ширина в 3 раза меньше длины, можно воспользоваться умножением числа на 3, чтобы найти ширину. Затем умножим длину на ширину и получим площадь поля.
Таким образом, занятия по математике в 5 классе позволяют развивать навыки решения задач, составлять уравнения и находить ответы на интересные вопросы. Решение подобных задач помогает ученикам улучшить свои навыки в математике и готовиться к большим и сложным заданиям, которые предстоят в школе.
- § Как правильно заниматься дома
- § Задания для 5 класса на тему «Натуральные числа»
- Задания на тему «Сравнения натуральных чисел»
- § Задания на тему «Сложение вычитания натуральных чисел»
- § Задания на тему «Луч, прямая, отрезок»
- § Задания на тему «Уравнения»
- § 3адания на тему «Квадрат и куб числа»
- § Задания на тему «Обыкновенные дроби»
- § Задания на тему «Сложение и вычитание обыкновенных дробей»
- § Задания на тему «Умножение и деление обыкновенных дробей»
- § Задания на тему «Десятичные дроби»
- § Задания на тему «Сложение и вычитание десятичных дробей»
- § Задания на тему «Умножение и деление десятичных дробей»
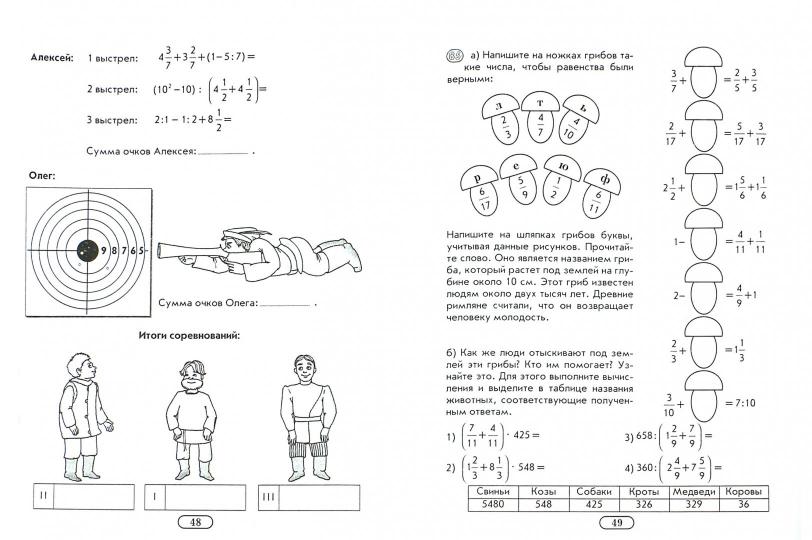
- ✍ 3адание 3
§ Как правильно заниматься дома
Для эффективных занятий дома важно создать подходящую обстановку и правильно организовать время.
Во-первых, выберите удобное место, где вы сможете сосредоточиться и не будете отвлекаться. Сделайте так, чтобы ваш рабочий стол был чистым и аккуратным: все необходимые пособия и учебники должны лежать в доступном месте. Также не забудьте о хорошем освещении для комфортного чтения и решения задач.
Во-вторых, составьте план занятий. Определите, какие задания нужно выполнить, и распределите время равномерно. Не забудьте о перерывах – они помогут вам отдохнуть и сохранить концентрацию внимания.
Одним из основных элементов учебного процесса является повторение пройденного материала. Для этого можно использовать различные методы, такие как составление таблиц, сравнение чисел, решение уравнений и дробей. Например, по заданию «Вычислить произведение двух чисел» можно составить таблицу умножения, где строки – это числа от 1 до 10, а столбцы – тоже числа от 1 до 10. В каждой ячейке таблицы будет указано произведение двух чисел. Затем можно решать уравнение, чтобы найти значения пропущенных чисел.
Также стоит обратить внимание на разделительные задачи. Например, задание «Найдите разность между длиной двух отрезков» можно решить следующим образом: возьмем два отрезка разной длины, например, 5 см и 8 см. Найдем их разность, вычитая из большего числа меньшее: 8 — 5 = 3. Таким образом, разность между длиной этих отрезков равна 3 см.
Для разнообразия заданий можно использовать задачи на примерах из реальной жизни. Например, по заданию «Составьте уравнение для вычисления количества штук грибов, если известно количество грибов в каждой корзине и общее количество корзин» можно решить следующим образом: пусть в каждой корзине лежит по 10 грибов, а всего имеется 5 корзин. Тогда общее количество грибов можно вычислить, умножив количество грибов в каждой корзине на общее количество корзин: 10 * 5 = 50 грибов.
Также можно использовать задачи на измерение длины или площади. Например, по заданию «Найдите площадь квадрата, если известна длина его стороны» можно решить следующим образом: пусть сторона квадрата равна 4 см. Тогда площадь квадрата будет равна произведению длины его стороны на саму себя: 4 * 4 = 16 см².
Таким образом, чтобы правильно заниматься дома, необходимо создать комфортные условия, составить план занятий, использовать различные методы и подходы к решению задач. И самое главное – не откладывать дела на потом, делать занятия регулярно и не забывать отдыхать!
§ Задания для 5 класса на тему «Натуральные числа»

Одной из задач, которую решает 5 класс, является задача о сравнении натуральных чисел. Например, нужно определить, какое из двух чисел больше или меньше. Для решения таких задач важно знать правила сравнения чисел: если у числа больше разрядов, то оно больше; если все разряды равны, а последнее, самое правое, отличается, то больше число будет то, у которого это разряд больше.
В другом задании ребенку предлагается составить число, которое будет в несколько раз больше или меньше данного. Например, если дано число 25, то нужно написать число, которое будет в два раза больше или в два раза меньше.
В одной задаче ребенку было известно, что мама заплатила за новый автомобиль сумму, которая составляет 6 500 000 рублей. Ребенок должен был сделать вывод, что известно ему наперёд.
Задача для самостоятельного решения: на огороде у Лены растут 12 кустов капусты и 8 штук грибов. На таком же огороде растут 20 кустов капусты. Сколько штук грибов растет на таком же огороде?
Одной из задач, которые ребенок решает во втором классе, являются задачи на умножение и деление с использованием таблицы умножения. Например, ребенку задается вопрос: сколько будет 8 умножить на 9. Чтобы найти ответ, нужно использовать таблицу умножения.
В одной задаче ребенку предлагается составить уравнение для нахождения неизвестного числа. Например, ребенку дают известное число, а нужно составить уравнение, в котором нужно найти неизвестное число.
Одной из задач, которые ребенок решает в пятом классе, являются задачи на десятичные дроби. Например, ребенку дают числа 3,75 и 5,6 и нужно определить, какое из них больше или меньше.
Другая задача предлагает ребенку найти количество деревьев на участке. Для решения этой задачи нужно знать, что количество деревьев на участке обозначается числом.
Задача для самостоятельного решения: Толя и его друг пошли в сад. Путь до сада составляет 2 километра. Они решили пройти пешком и разделить путь на две равные части. Сколько каждый из них должен пройти?
Другая задача предлагает ребенку определить длину ткани. Например, ребенку дают кусок ткани длиной 3 метра и нужно определить, на сколько частей нужно разделить его, чтобы каждая часть была длиной 0,6 метра.
Задания на тему «Сравнения натуральных чисел»

Чтобы научиться сравнивать натуральные числа, необходимо знать их порядок. Например, для сравнения чисел 568 и 425, нужно сначала посмотреть первую цифру с левой стороны, а затем вторую и третью. В данном случае, цифра 5 в числе 568 больше цифры 4 в числе 425. Поэтому число 568 больше числа 425.
Если у чисел в самой левой разрядной цифре одинаковые цифры, то сравнивают следующую цифру справа. Например, если мы сравниваем числа 823 и 815, то сначала сравниваем 8 и 8, а затем сравниваем 2 и 1. В данном случае, 2 больше 1, поэтому число 823 больше числа 815.
Чтобы сравнить два числа, которые имеют разное количество разрядов, необходимо добавить нули к меньшему числу, чтобы они стали одинаковой длины. Например, чтобы сравнить числа 76 и 542, нужно превратить число 76 в число 076. Затем мы сравниваем почередно цифры и видим, что 5 больше 0, поэтому число 542 больше числа 076.
Сравнение натуральных чисел также может быть использовано для определения отношений «больше», «меньше» и «равно». Например, чтобы ответить на вопрос, сколько яблонь больше – 56 или 89, необходимо сравнить числа 056 и 089. В данном случае, число 089 больше числа 056. То есть, 89 яблонь больше, чем 56 яблонь.
Если нужно найти разницу между количеством каких-то предметов, можно использовать сравнение натуральных чисел. Например, если у ребенка было 15 ящиков с яблоками, а потом он отдал 7 ящиков, необходимо вычислить, сколько ящиков осталось. Для этого нужно вычесть 7 из 15 и получить результат 8.
В задачах на сравнение натуральных чисел также может быть использовано умножение и деление. Например, если необходимо найти произведение двух чисел, можно использовать сравнение и умножение. Например, чтобы найти произведение чисел 5 и 7, можно составить равенство: 5 * 7 = 35. Значит, произведение чисел 5 и 7 равно 35.
Также в задачах на сравнение натуральных чисел могут быть использованы дроби. Например, чтобы решить задачу о длине отрезка, который лежит перед велосипедистом, можно использовать сравнение и деление. Например, если велосипедист проехал 375 метров за 5 минут, то его скорость можно найти, разделив 375 на 5 и получив результат 75 метров в минуту.
В задачах на сравнение натуральных чисел могут быть использованы также математические формулы. Например, чтобы решить задачу о количестве грушевых деревьев, можно использовать сравнение и квадрат. Например, если известно, что одно грушевое дерево дает 20 кг груш, а мы собрали 600 кг груш, то можно найти количество грушевых деревьев, разделив 600 на 20 и получив результат 30 грушевых деревьев.
В задачах на сравнение натуральных чисел часто используются слова «больше», «меньше», «равно». Например, чтобы решить задачу о сравнении количества яблок и груш, можно использовать сравнение и слова «больше» и «меньше». Например, если известно, что количество яблок в корзине больше количества груш в корзине, можно сказать, что яблок больше, чем груш.
Таким образом, задания на тему «Сравнения натуральных чисел» помогут развить навыки сравнения чисел, а также применение математических операций в решении задач.
§ Задания на тему «Сложение вычитания натуральных чисел»
Одной из основных операций в математике является сложение и вычитание натуральных чисел. Это важные навыки, которые необходимо освоить в начальной школе. В данном разделе представлены задания, которые помогут ученикам 5 класса закрепить данную тему.
Задания на сложение представлены в виде примеров, где необходимо найти сумму двух или более цифр. Например, задача может быть сформулирована следующим образом: «Толя купил в магазине 3 рулона ткани длиной 5 метров каждый. Сколько всего метров ткани купил Толя?». Чтобы решить эту задачу, необходимо сложить длины всех рулонов: 5 + 5 + 5 = 15. Ответом будет число 15 метров.
Задания на вычитание связаны с определением разности двух чисел. Например, рассмотрим задачу: «У Маши было 10 капуст, а она продала 5. Сколько капуст осталось у Маши?». В данном случае необходимо из общего количества капуст (10) вычесть количество проданных капуст (5). Разность будет составлять 5 капуст.
Иногда для решения задач по сложению и вычитанию необходимо использовать дробные числа. Например, задача может быть такой: «Между двумя садами расстояние составляет 2,5 км. Одной части пути между садами Лена прошла пешком, а остальную часть – на велосипеде. Пешком она прошла 1,2 км. Какое расстояние Лена проехала на велосипеде?». Чтобы решить данную задачу, необходимо от общего расстояния (2,5 км) отнять пройденное пешком (1,2 км). Ответом будет число 1,3 км.
Также в заданиях на сложение и вычитание могут использоваться большие числа, например, тысячи и сотни. Например, задача может быть сформулирована следующим образом: «Мама сделала 8 пирогов. Для каждого пирога было использовано 3 яблока. Сколько всего яблок было использовано для пирогов?». Чтобы решить эту задачу, необходимо умножить количество пирогов (8) на количество яблок в каждом пироге (3): 8 * 3 = 24. Ответом будет число 24 яблока.
§ Задания на тему «Луч, прямая, отрезок»
Задание 1: На столе лежит рулон с капустой. Пешеход решил измерить его длину. Как можно это сделать?
Задание 2: В ящиках лежат яблоки, груши и сливы. Толя прочитал, что весь слив лежит в двух ящиках, а количество груш в одном из ящиков больше, чем яблок. Сколько яблок и груш лежит в ящиках?
Задание 3: В руке у мамы третий коробок. Если на каждый из восьми коробков будет ложить по спичке, останется 5 спичек. А если на каждый из семи коробков будет ложить по медали, останется 6 медалей. Какое количество спичек и медалей загадано в самом третьем коробке?
Задание 4: Лена решила сделать занятия по математике. В учебнике она прочитала, что для сложения и вычитания обыкновенных дробей нужно найти общий знаменатель. Затем нужно прибавить или вычесть числители дробей и оставить знаменатель неизменным. А как делать в случае умножения и деления дробей? Какие решения она может использовать?
Задание 5: На поляне растут яблони и грибы. Количество яблонь в 2 раза больше, чем грибов. Если отдельно посчитать количество яблонь и грибов, то их в сумме будет 12 штук. Найдите количество яблонь и грибов на поле.
Задание 6: Школьники измеряют отрезок линейкой. Длина отрезка 80 метров. Какую его часть составляет отрезок длиной 25 метров?
Ответы на задания:
- Задание 1: Измерить длину рулона можно с помощью линейки или мерной ленты.
- Задание 2: Количество яблок и груш в ящиках неизвестно.
- Задание 3: В третьем коробке может быть 27 спичек и 34 медали.
- Задание 4: Для умножения дробей необходимо умножить числители и знаменатели обоих дробей. Для деления дробей необходимо умножить первую дробь на обратную второй дроби.
- Задание 5: На поле может быть 8 яблонь и 4 гриба.
- Задание 6: Отрезок длиной 25 метров составляет 1/4 от всего отрезка длиной 80 метров.
§ Задания на тему «Уравнения»
Уравнение – это математическое выражение, в котором две части разделены знаком равенства. В уравнении могут быть представлены числа, дроби или их комбинации. Задания по уравнениям помогут учащемуся развить навыки решения математических задач, а также научат применять различные математические операции для нахождения неизвестного значения.
В заданиях на уравнения ученику предлагается сделать несколько шагов для вычисления значения неизвестной величины. Например, в первом задании ученику нужно сложить два числа и сравнить сумму с заданным результатом. Затем он должен определить, какое число было записано в первой части уравнения.
Во втором задании ученику предлагается решить уравнение, в котором присутствуют десятичные числа. Он должен определить значения двух неизвестных частей, а затем выполнить умножение и вычитание для получения правильного ответа.
В третьем задании ученику нужно решить уравнение, в котором присутствуют дроби. Он должен определить значения обоих частей уравнения и выполнить умножение и деление для получения правильного ответа.
Задания на тему «Уравнения» помогут ученикам развить логическое мышление, математическую интуицию и навыки решения математических задач. Они также помогут ученикам понять, как применять математические операции для нахождения неизвестных значений в уравнении.
§ 3адания на тему «Квадрат и куб числа»

Во время изучения математики в школе ученикам часто задаются задания на вычисление квадратов и кубов чисел. Это помогает им закрепить знания о свойствах чисел и развить навыки аналитического мышления.
Например, учитель может предложить ученикам задачу по определению количества ящиков, необходимых для упаковки определенного количества грибов. Если известно, что в одном ящике помещается 25 грибов, а всего нужно упаковать 125 грибов, то ученики могут воспользоваться знанием о свойствах кубов чисел и вычислить, что нужно 5 ящиков.
Другим примером задачи на вычисление квадрата числа может быть задание по определению длины пути, который преодолел пешеход. Если известно, что путь, который он прошел, был равен 9 километрам, то можно найти квадрат числа 9 и получить ответ — 81, что будет являться длиной пути в квадратных километрах.
Также ученикам могут предлагаться задачи на составление выражений или нахождение длины отрезка. Например, задача может состоять в том, чтобы найти длину отрезка между двумя точками на числовой оси, зная координаты этих точек. Для решения такой задачи ученикам нужно воспользоваться формулой для нахождения расстояния между двумя точками на числовой оси, которая называется формулой модуля разности.
§ Задания на тему «Обыкновенные дроби»
Во время занятий по математике в 5 классе детям необходимо изучать и понимать такую тему, как обыкновенные дроби. Обыкновенными дробями называются числа, представленные дробью, где числитель и знаменатель — целые числа. Для вашей домашней работы предлагается несколько заданий, которые помогут усвоить эту тему более глубоко и лучше понять ее применение в практике.
- Составить уравнение: Вы путешествуете на автомобиле. За третий час вы проехали 2/5 всего пути. Зная, что весь путь составляет 625 километров, найдите сколько километров вы проехали за 3 часа.
- Работа с рулоном: Второй рулон обоев имеет длину 120 метров. В первом рулоне обои были распределены по стенам комнаты, затем второй рулон использовали для дальнейшей отделки. Какая часть обоев осталась неиспользованной?
- Решение уравнений: В самолете находились 86 пассажиров. 2/3 пассажиров сели сначала в Казани, затем еще 1/4 из Москвы. Сколько пассажиров прилетело в пункт назначения отдельно из Казани и отдельно из Москвы?
- Вычисления с десятичными дробями: В ящиках лежит 3,75 кг грушевых. Для продажи их нужно разложить в пакеты по 0,5 кг. Сколько пакетов нужно сделать?
- Работа с отрезком: Ребенок загадал число на числовой прямой между двумя другими числами. Если одно число равно -5/6, а второе число равно 1/3, то какое число загадано ребенком?
Решения этих заданий помогут вам лучше понять применение обыкновенных дробей в различных ситуациях и расширить навыки работы с ними. Успехов в изучении темы обыкновенных дробей!
§ Задания на тему «Сложение и вычитание обыкновенных дробей»
Для выполнения заданий по математике по теме «Сложение и вычитание обыкновенных дробей» вам потребуется знание основных свойств и правил работы с дробями. Обыкновенная дробь представляет собой дробь, в которой числитель и знаменатель являются целыми числами и знаменатель не равен нулю.
В первом задании вам предлагается сложить две обыкновенные дроби. Для этого нужно найти общий знаменатель, а затем привести дроби к единому знаменателю. После этого сложите числители дробей и результат запишите в форме обыкновенной дроби с найденным общим знаменателем.
Во втором задании вам нужно вычесть одну обыкновенную дробь из другой. Алгоритм вычитания обыкновенных дробей аналогичен алгоритму сложения. Найдите общий знаменатель, приведите дроби к единому знаменателю и вычитайте числители.
В третьем задании вам предлагается решить уравнение с дробной частью. Необходимо найти значение неизвестного числа, чтобы уравнение стало верным. Для этого сложите или вычтите обыкновенные дроби и найдите значение неизвестного.
Все задания на тему «Сложение и вычитание обыкновенных дробей» позволят вам отработать навыки работы с дробями, а также развить логическое мышление и умение решать математические задачи.
§ Задания на тему «Умножение и деление обыкновенных дробей»
Для успешного выполнения заданий по математике в 5 классе необходимо хорошо понимать понятия дроби, умножения и деления обыкновенных дробей. Например, дробь представляет собой отношение двух чисел, числитель и знаменатель, например, 2/3. Умножение и деление обыкновенных дробей позволяет производить арифметические операции с этими числами, чтобы найди их произведение или частное.
Во время занятий по математике одной из задач может быть вычислить, например, длину отрезка, который проехал велосипедист за 45 минут со скоростью 10 км/час. Для решения этой задачи необходимо умножить время на скорость, чтобы найти длину отрезка в километрах.
Другой задачей может быть произведение двух десятичных дробей. Например, необходимо вычислить произведение 0,75 и 0,2. Для решения этой задачи необходимо умножить дроби и получить результат в виде десятичной дроби.
Еще одним примером задачи может быть задача про сбор яблок с яблонь. Необходимо вычислить, какую часть яблок лене досталось, если она собрала 3/5 яблок, а весь урожай составлял 1000 яблок.
Для успешного выполнения задач по умножению и делению обыкновенных дробей необходимо уметь составить и решить математические выражения, которые связаны с этой темой. Например, можно составить уравнение, в котором загадано произведение двух дробей и необходимо найти одну из дробей.
Также в задачах по умножению и делению обыкновенных дробей важно уметь правильно использовать умножение и деление, чтобы выразить одну дробь через другую, например, если нужно выразить третью часть от яблок через количество яблок, то нужно делить.
Тема умножения и деления обыкновенных дробей может быть представлена в виде таблицы или списка, где будут перечислены все задачи, которые необходимо решить, и указана необходимая для этого формула или правило. Например, для решения задачи про яблоки можно использовать пропорцию или правило трех частей.
§ Задания на тему «Десятичные дроби»
Одно из заданий, связанных с десятичными дробями, может быть следующим: например, чему равно 1,7 + 3,9? Для решения этого уравнения нужно сложить оба числа таким же образом, как обычно складываются целые числа. Сначала сложите десятки, затем единицы, а затем десятые и сотые части чисел.
Другое задание можно сформулировать так: в саду росло 12 деревьев. Толя загадал, что часть деревьев составляют десятичные дроби, обозначая их длину в метрах. Для каждого дерева он вычитал из длины ствола 0,5 метра, а затем умножал полученную разность на 1,2. Какое количество деревьев имеют дробную длину ствола?
Еще одно задание: автомобиль и велосипедист движутся по одному пути. Велосипедист начал движение на 60 метров позже автомобиля и движется с постоянной скоростью. Автомобиль же движется с постоянной скоростью в 2 раза больше скорости велосипедиста. Через некоторое время автомобиль догнал велосипедиста. Определите расстояние, которое преодолел автомобиль, к моменту догоняния.
Еще одно задание: вам необходимо найти произведение двух десятичных дробей. Возьмем, например, дроби 0,3 и 0,4. Сначала каждое из чисел представим в виде обыкновенной дроби: 0,3 = 3/10 и 0,4 = 4/10. Затем перемножим числитель одной из дробей на числитель другой дроби, а знаменатель первой дроби на знаменатель второй дроби. В результате получим произведение 3*4 = 12 для числителя и 10*10 = 100 для знаменателя. Таким образом, ответом будет десятичная дробь 12/100, которая равна 0,12.
§ Задания на тему «Сложение и вычитание десятичных дробей»
Для выполнения заданий по сложению и вычитанию десятичных дробей необходимо знать правила работы с этими числами. Десятичная дробь состоит из двух частей: целой и дробной. Целая часть отделяется запятой или точкой от дробной.
Рассмотрим пример задачи на сложение десятичных дробей. Представьте, что у вас есть 3,2 кг яблок и 1,8 кг грушей. Сколько вы получите фруктов, если их сложить? Чтобы найти ответ, сложите десятичные дроби: 3,2 + 1,8 = 5. Таким образом, вы получите 5 кг фруктов.
В задачах на вычитание десятичных дробей действуем по аналогии. Например, у вас есть 5,7 кг капусты, а нужно использовать только 2,3 кг. Сколько килограммов капусты останется? Чтобы найти ответ, вычитаем одну десятичную дробь из другой: 5,7 — 2,3 = 3,4. Ответом будет 3,4 кг капусты, которая останется.
Для решения задач на сложение и вычитание десятичных дробей можно использовать названные выше методы. Важно помнить, что сложение и вычитание выполняются в том же порядке, что и для обычных чисел. Также необходимо уметь работать с дробями и правильно выполнять действия.
§ Задания на тему «Умножение и деление десятичных дробей»

Умножение и деление десятичных дробей – важные операции, которые необходимо уметь выполнять. При выполнении этих операций используются особые правила и свойства, с помощью которых можно упростить расчеты и получить правильный ответ.
Одно из заданий на умножение десятичных дробей может быть связано с решением садовой задачи. Например, в саду загадано количество яблонь. Если известно, что на каждой яблоне растет по 0,75 метра яблок, то необходимо вычислить, какое количество яблок будет на всех деревьях сада.
Для решения задач на деление десятичных дробей можно использовать пример с распределением капусты между учениками. Например, ученику Лене необходимо разделить 2,5 кг капусты на 5 равных частей. Чтобы найти вес каждой части, нужно поделить 2,5 на 5.
Другим примером задачи на деление десятичных дробей может быть рассмотрение отдельного отрезка ткани. Если длина отрезка составляет 3,6 метра, а нужное количество рулонов по 0,9 метра, то необходимо вычислить, сколько рулонов ткани будет достаточно для покрытия всей длины отрезка.
Умножение и деление десятичных дробей также можно рассматривать с помощью выражений. Например, чтобы найти произведение двух десятичных дробей, можно умножить числа перед запятой отдельно, а затем числа после запятой отдельно. Полученные результаты необходимо объединить, чтобы получить правильный ответ.
Тесно связанные задачи на умножение и деление десятичных дробей могут быть интересными и полезными для развития математических навыков у учеников. С помощью таких заданий дети смогут закрепить и углубить свои знания в данной теме и научиться применять их на практике.
✍ 3адание 3
Одним из методов решения математических задач является использование знания о сложении десятичных чисел. Представим ситуацию: ребенок идет пешком по пути от дома до школы, который растянулся на несколько кварталов.
Мама дала ему задание: найти длину всего пути. Ребенок знает, что расстояние от дома до школы составляет 1200 метров. Затем мама говорит ему, что он прошел часть пути, равную 3/4 от всего расстояния. Ребенок хочет найти, сколько метров он уже прошел и какое количество метров осталось.
Чтобы решить эту задачу, нужно найти длину всего пути и выразить ее в виде десятичного числа. Затем, чтобы найти, сколько метров ребенок прошел, нужно взять это число и умножить на дробь 3/4. Для этого можно воспользоваться уравнением: длина пути умножить на 3/4.
Ребенок делает вычисления и получает, что он прошел 900 метров. Чтобы узнать, сколько метров ему осталось пройти, нужно вычесть 900 из 1200. В результате получается, что осталось пройти 300 метров.
Таким образом, решение задачи состоит в нахождении длины всего пути, вычислении, сколько метров ребенок уже прошел и сколько метров осталось пройти.